题目内容
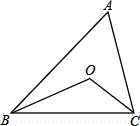
【题目】如图,在![]() ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A ![]() 60°,求∠BOC的度数;
60°,求∠BOC的度数;
(2)若∠A ![]() 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?
(3)若∠A ![]() 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
【答案】(1)∠BOC![]() 120°;(2)∠BOC
120°;(2)∠BOC![]() 140°;(3)∠BOC=150°;(4)∠BOC=90°+
140°;(3)∠BOC=150°;(4)∠BOC=90°+![]() ∠A
∠A
【解析】
(1)根据BO、CO分别平分∠ABC和∠ACB可得: ∠CBO+∠BCO的值,再根据三角形内角和得出∠BOC;
(2)、(3)同理(1)可求得;
(4)根据(1)-(3)规律可得.
(1)∵BO、CO分别平分∠ABC和∠ACB.∠A ![]() 600
600
∴∠CBO+∠BCO![]()
![]() (1800
(1800![]() ∠A)
∠A)![]()
![]() (1800
(1800![]() 600)
600)![]() 600
600
∴∠BOC![]() 1800
1800![]() (∠CBO+∠BCO)
(∠CBO+∠BCO)![]() 1800
1800![]() 600
600![]() 1200
1200
(2)同理,若∠A ![]() 1000, 则∠BOC
1000, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1400
1400
(3)同理,若∠A ![]() 1200, 则∠BOC
1200, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1500
1500
(4)由(1)、(2)、(3),发现:∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A

【题目】2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校时捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)根据以上信息,解答下列问题:
(1)写出p与n的关系式;
(2)当p=125时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由(2)确定,则再次提供的捐款最多又可以援助多少所学校?
分配顺序 | 分配数额(单位:万元) | |
帐篷费用 | 教学设备费用 | |
第1所学校 | 5 | 剩余款的 |
第2所学校 | 10 | 再剩余款的 |
第3所学校 | 15 | 再剩余款的 |
… | … | … |
第(n﹣1)所学校 | 5(n﹣1) | 再剩余款的 |
第n所学校 | 5n | 0 |