题目内容
 在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.分析:过点B作BM⊥FD于点M,解直角三角形求出BC,在△BMC值解直角三角形求出CM,BM,推出BM=DM,即可求出答案.
解答:解:
过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC tan60°=10
,
∵AB∥CF,∴∠BCM=∠ABC=30°.
∴BM=BC•sin30°=10
×
=5
,
CM=BC•cos30°=10
×
=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5
,
∴CD=CM-MD=15-5
.

过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC tan60°=10
| 3 |
∵AB∥CF,∴∠BCM=∠ABC=30°.
∴BM=BC•sin30°=10
| 3 |
| 1 |
| 2 |
| 3 |
CM=BC•cos30°=10
| 3 |
| ||
| 2 |
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5
| 3 |
∴CD=CM-MD=15-5
| 3 |
点评:本题考查了解直角三角形的应用,关键是能通过解直角三角形求出线段CM、MD的长.

练习册系列答案
相关题目
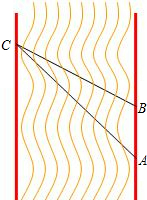 在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈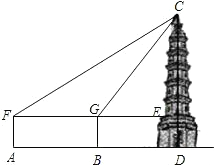 时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.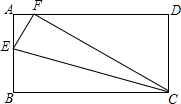 在一次数学活动课上,张明同学将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,如图所示,已知CD=8cm,BE=5cm,则AD=
在一次数学活动课上,张明同学将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,如图所示,已知CD=8cm,BE=5cm,则AD= 在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上. 在一次数学活动课上,王老师给学生发了一块长40cm,宽30cm的长方形纸片(如图),要求折成一个高为5cm的无盖的且容积最大的长方体盒子.
在一次数学活动课上,王老师给学生发了一块长40cm,宽30cm的长方形纸片(如图),要求折成一个高为5cm的无盖的且容积最大的长方体盒子.