题目内容
10.如图1,在4×4的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点.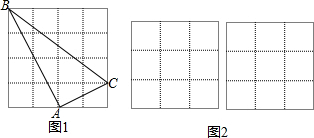
(1)填空:AB=2$\sqrt{5}$,∠BAC=90°.
(2)请在图2中的两个3×3的正方形方格中各画一个和△ABC相似但不全等的格点三角形.
分析 (1)利用网格结合勾股定理得出答案即可;
(2)利用相似三角形的性质得出符合题意的图形即可.
解答  解:(1)AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
解:(1)AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵AB2+AC2=20+5=25,BC2=25,
∴AB2+AC2=BC2,
∴∠BAC=90°,
故答案为:2$\sqrt{5}$,90;
(2)如图所示:△DEF和△MNG都是符合题意的图形.
点评 此题主要考查了相似变换,利用勾股定理以及相似三角形的性质得出是解题关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
20.下列长度的三条线段能组成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 4,6,8 | D. | 5,5,11 |
20. 如图,数轴上有A,B,C,D四个点,其中绝对值为2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值为2的数对应的点是( )
 如图,数轴上有A,B,C,D四个点,其中绝对值为2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值为2的数对应的点是( )| A. | 点A与点C | B. | 点A与点D | C. | 点B与点C | D. | 点B与点D |
 如图,在Rt△ACB中,∠ACB=90°,以BC为直径的⊙O与AB的另一个交点为D,点E为AC的中点.
如图,在Rt△ACB中,∠ACB=90°,以BC为直径的⊙O与AB的另一个交点为D,点E为AC的中点.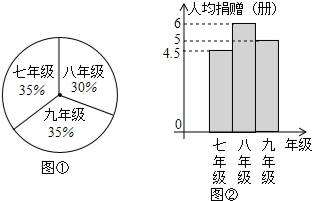
 一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2=95°.
一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2=95°.