题目内容
9.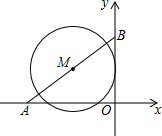 如图直角坐标系中,已知A(-8,0),B(0,6),点M在线段AB上.如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由.
如图直角坐标系中,已知A(-8,0),B(0,6),点M在线段AB上.如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由.
分析 设线段OB的中点为D,连结MD,根据三角形的中位线定理求出MD的长,再由平行线的性质即可得出结论.
解答  解:直线OB与⊙M相切.
解:直线OB与⊙M相切.
理由:设线段OB的中点为D,连结MD.
∵点M是线段AB的中点,
∴MD∥AO,MD=$\frac{1}{2}$AO=$\frac{1}{2}$×8=4.
∴∠MDB=∠AOB=90°,
∴MD⊥OB,
∴直线OB与⊙M相切.
点评 本题考查的是直线与圆的位置关系,熟知直线与圆相切的条件是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.表是某周的生产情况(超产为正、减产为负):
(1)根据记录可知前三天共生产599辆;
(2)产量最多的一天比产量最少的一天多26辆;
(3)该厂实行每周计件工资制,每生产一辆车可得50元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -4 | +12 | -10 | +16 | -8 |
(2)产量最多的一天比产量最少的一天多26辆;
(3)该厂实行每周计件工资制,每生产一辆车可得50元,那么该厂工人这一周的工资总额是多少?
1.下列运算中正确的是( )
| A. | m÷n•m=m | B. | m÷n•$\frac{1}{m}$=m | C. | $\frac{1}{m}$÷m•m=1 | D. | n÷m•m=n |
 如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)
如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2) 如图,AB=AC=AD,这可以说明,点B,C和D都在以点A为圆心,以AB为半径的圆上.
如图,AB=AC=AD,这可以说明,点B,C和D都在以点A为圆心,以AB为半径的圆上.