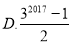题目内容
为求1+2+22+23+……+22007+22008 的值,可令S=1+2+22+23+......+22007+22008 ,则2S=2+22+23+……+22008+22009 ,因此2S-S=22009 -1,∴S=22009 -1,∴ 1+2+22+23+……+22007+22008 =22009 -1.仿照以上推理计算出1+3+32+33+……+32016+32017的值是( )
A. 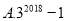 B.
B. 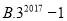 C.
C. 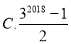 D.
D. 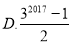
练习册系列答案
相关题目
题目内容
为求1+2+22+23+……+22007+22008 的值,可令S=1+2+22+23+......+22007+22008 ,则2S=2+22+23+……+22008+22009 ,因此2S-S=22009 -1,∴S=22009 -1,∴ 1+2+22+23+……+22007+22008 =22009 -1.仿照以上推理计算出1+3+32+33+……+32016+32017的值是( )
A. 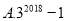 B.
B. 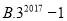 C.
C. 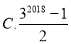 D.
D.