题目内容
已知抛物线m:![]() ,顶点为A,将抛物线m绕着
,顶点为A,将抛物线m绕着
点(-1,0) 旋转180°后得到抛物线n,顶点为C.
(1)当a=1时.试求抛物线n的顶点C的坐标,再求它的解析式;
(2)在(1)中,请你分别在抛物线m、n上各取一点B、D(除点A、C外),
使得四边形ABCD成为平行四边形(直接写出所取点的坐标);
(3)抛物线n与抛物线m的对称轴的交点为P,①若AP=6,试求a的值.
②抛物线m与抛物线n的对称轴的交点为Q,若四边形APCQ能成为菱形,直接求出菱形的周长;若四边形APCQ不能成为菱形,说明理由。


(1)当a=1时,抛物线m的解析式为![]() ,
,
顶点A(1,-1), 点A(1,-1)绕着点(-1,0)旋转180°后
所得点C坐标为(-3, 1), …………………………………………………………2分
根据题意可得抛物线n的解析式为![]() ,或
,或![]() . …4分
. …4分

(2)如:B(2,0)与D(-4,0)
或B(0,0)与D(-2,0)
或B(3, 3)与.D(-5,-3)
(答案不唯一)…………………………6分
(3)①设抛物线n的解析式为![]()
方法一:
∵A(1,-1), 当x=1时,y==-16a+1,
∴点P ( 1, -16a+1 ) …………………7分
∴ ![]() , ………………8分
, ………………8分
当1-(-16a + 1 )=6时,解得 a=![]() ,……………………………9分
,……………………………9分
当 (-16a + 1 ) -1=6时,16a=-4,a=![]() ,
,
∴![]() 或
或![]() . …………………………10分
. …………………………10分
方法二:①
∵AP=6 ∴P为(1,-7)或(1,5) …………………………8分
当P为(1,-7)时,代入抛物线n的解析式![]() 得
得![]() …………9分
…………9分
当P为(1,5)时, 代入抛物线n的解析式![]() 得
得![]() …………10分
…………10分



(3)② 能成为菱形,菱形的周长等于20. …

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 已知抛物线y=ax2+bx+c过点C(0,3),顶点P(2,-1),直线x=m(m>3)交x轴于点D,抛物线交x轴于A、B两点(如图10).
已知抛物线y=ax2+bx+c过点C(0,3),顶点P(2,-1),直线x=m(m>3)交x轴于点D,抛物线交x轴于A、B两点(如图10).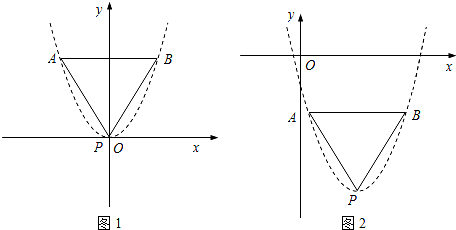
 的顶点A到
的顶点A到 轴的距离为3, 与
轴的距离为3, 与 轴交于C、D两点.
轴交于C、D两点. ,求点B的坐标.
,求点B的坐标. (a≠0)的顶点在直线
(a≠0)的顶点在直线 上,且过点A(4,0).
上,且过点A(4,0). 的值最大,请直接写出点D的坐标.
的值最大,请直接写出点D的坐标.