题目内容
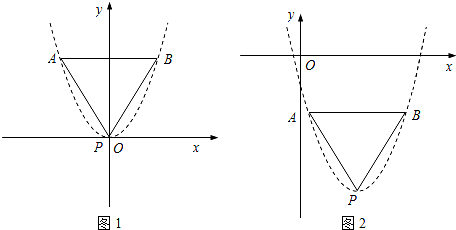
如图1,已知抛物线y=ax2的顶点为P,A、B是抛物线上两点,AB∥x轴,△PAB是等边三角形.(1)若点B的横坐标为
| 3 |
(2)①如图2,将(1)中抛物线进行平移,使点P的坐标变为(m,n),其他条件不变,请猜想△PAB的边长;
②若将抛物线“y=ax2”,改为抛物线“y=2x2-8x-2”,其他条件不变,求△PAB的边长;
(3)已知等边△MCD,CD∥x轴,抛物线l经过△MCD 的三个顶点,若点M的坐标为(m,n),△MCD的边长为2b,请直接写出抛物线l的函数表达式.(用含m、n、b的式子表示)
分析:(1)根据已知条件“△PAB是等边三角形,AB∥x轴,设AB交y轴于E”推知,△PEB是直角三角形,在直角三角形内根据点B的坐标求得AE=BE=
;然后由等边三角形ABC的三个内角都是60°的性质求得∠PBE=60°,所以根据特殊角的三角函数求得点A的坐标(-
,3);最后由二次函数图象上点的坐标特征、待定系数法求二次函数解析式;
(2)①根据平移的性质:平移不改变图形的形状和大小,来回答问题;
②第一种方法:平移抛物线y=2x2-8x-2,使P与O重合,得抛物线y=2x2,设相应的等边三角形为A'B'O,B'点坐标为(k,
k),然后利用二次函数图象上坐标的特征求得关于k的一元二次方程,解方程即可(由平移不改变图形的形状和大小决定k值);
第二种方法:y=2x2-8x-2可变形为y=2(x-2)2-10,从而求得点P的坐标;再由已知条件“△PAB是等边三角形,AB∥x轴”设B点坐标为(2+k,-10+
k);然后利用二次函数图象上坐标的特征求得关于k的一元二次方程,解方程即可(由平移不改变图形的形状和大小决定k值);
(3)由(1)、(2)可以直接写出抛物线l的函数表达式.(用含m、n、b的式子表示).
| 3 |
| 3 |
(2)①根据平移的性质:平移不改变图形的形状和大小,来回答问题;
②第一种方法:平移抛物线y=2x2-8x-2,使P与O重合,得抛物线y=2x2,设相应的等边三角形为A'B'O,B'点坐标为(k,
| 3 |
第二种方法:y=2x2-8x-2可变形为y=2(x-2)2-10,从而求得点P的坐标;再由已知条件“△PAB是等边三角形,AB∥x轴”设B点坐标为(2+k,-10+
| 3 |
(3)由(1)、(2)可以直接写出抛物线l的函数表达式.(用含m、n、b的式子表示).
解答: 解:(1)∵△PAB是等边三角形,AB∥x轴,设AB交y轴于E,
解:(1)∵△PAB是等边三角形,AB∥x轴,设AB交y轴于E,
∴△PEB是直角三角形,AE=BE=
,∠PBE=60°,
∴∠BPE=30°,PB=2BE=2
,PE=3,
∴点B的坐标(
,3),点A的坐标(-
,3),(2分)
∵点B在抛物线y=ax2上,
∴3=(
)2a,解得:a=1,
∴抛物线的函数表达式为y=x2(4分);
(2)①∵平移不改变图形的形状和大小,
∴△PAB的边长仍为2
;(6分)
②方法一:平移抛物线y=2x2-8x-2,使P与O重合,得抛物线y=2x2,
设相应的等边三角形为A'B'O,B'点坐标为(k,
k),
∴
k=2k2,解得:k1=0(舍去),k2=
,A'B'=2k=
,
∵平移不改变图形的形状和大小,
∴△PAB的边长为
;(11分)
方法二:y=2x2-8x-2可变形为y=2(x-2)2-10,
∴P点坐标为(2,-10),由△PAB是等边三角形,AB∥x轴,
∴设B点坐标为(2+k,-10+
k),
∴-10+
k=2(2+k)2-8×(2+k)-2,
解得:k1=0(舍去),k2=
,AB=2k=
,
∴△PAB的边长为
;(11分)
(3)y=
(x-m)2+n或y=-
(x-m)2+n.(14分)
 解:(1)∵△PAB是等边三角形,AB∥x轴,设AB交y轴于E,
解:(1)∵△PAB是等边三角形,AB∥x轴,设AB交y轴于E,∴△PEB是直角三角形,AE=BE=
| 3 |
∴∠BPE=30°,PB=2BE=2
| 3 |
∴点B的坐标(
| 3 |
| 3 |
∵点B在抛物线y=ax2上,
∴3=(
| 3 |
∴抛物线的函数表达式为y=x2(4分);
(2)①∵平移不改变图形的形状和大小,
∴△PAB的边长仍为2
| 3 |
②方法一:平移抛物线y=2x2-8x-2,使P与O重合,得抛物线y=2x2,
设相应的等边三角形为A'B'O,B'点坐标为(k,
| 3 |
∴
| 3 |
| ||
| 2 |
| 3 |
∵平移不改变图形的形状和大小,
∴△PAB的边长为
| 3 |
方法二:y=2x2-8x-2可变形为y=2(x-2)2-10,
∴P点坐标为(2,-10),由△PAB是等边三角形,AB∥x轴,
∴设B点坐标为(2+k,-10+
| 3 |
∴-10+
| 3 |
解得:k1=0(舍去),k2=
| ||
| 2 |
| 3 |
∴△PAB的边长为
| 3 |
(3)y=
| ||
| b |
| ||
| b |
点评:本题考查了二次函数的综合题.其中涉及到的知识点有二次函数图象上点的坐标特征、待定系数法求二次函数解析式.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.