题目内容
在坡度为
的斜坡前6米处有一高度为10米的树，当太阳照射的倾斜角为45°时，求斜坡上的树影长．
【答案】分析：过点E作EF⊥CD于点F，则△ABD为等腰直角三角形，即可求得CD的长度，已知∠ECF和∠EDF，设EF的长度是x，利用三角函数即可表示出CF，FD，根据CD=CF+FD，即可得到一个关于x的方程，即可求得x的值，进而求得CE的长度．
解答：
解：过点E作EF⊥CD于点F．
∵△ABD为等腰直角三角形．
∴BD=10，
∴CD=10-6=4
∵
，
∴∠ECF=30°．
设EF=x，则CE=2x，
，DF=x，
∵CF+DF=CD，
∴
，
∴
，
则CE=2x=4
-4．
点评：本题是解直角三角形，坡度的问题，把求线段的长的问题转化为解方程的问题，体现了方程思想的应用．
解答：
解：过点E作EF⊥CD于点F．∵△ABD为等腰直角三角形．
∴BD=10，
∴CD=10-6=4
∵
，∴∠ECF=30°．
设EF=x，则CE=2x，
，DF=x，∵CF+DF=CD，
∴
，∴
，则CE=2x=4
-4．点评：本题是解直角三角形，坡度的问题，把求线段的长的问题转化为解方程的问题，体现了方程思想的应用．
练习册系列答案
相关题目
（2010•安庆二模）在坡度为
如图，已知斜坡AB长60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．（下面两小题的结果都精确到0.1米，参考数据：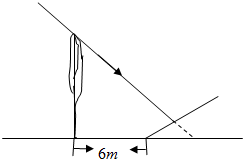
在坡度为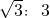
的斜坡前6米处有一高度为10米的树，当太阳照射的倾斜角为45°时，求斜坡上的树影长．
两小题的结果都精确到0.1米，参考数据：
≈1.732）
米；