Question

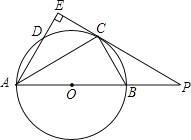
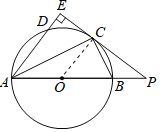
【题目】如图，AB是⊙O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC．

（1）求证：AC平分∠BAD；

（2）若AB=3，AC=2，求EC和PB的长．

Answer 1

【答案】（1）见解析；（2）EC=，PB=．

【解析】

（1）连接OC，如图，利用切线的性质得到OC⊥PE，则判断OC∥AE，所以∠DAC=∠OCA，然后利用∠OCA=∠OAC得到∠DAC=∠OAC；

（2）利用圆周角定理得到∠ACB=90°，再利用勾股定理计算出BC=2，再证明Rt△ABC∽Rt△ACE，利用相似比计算出EC=，接着利用勾股定理计算出AE=，然后证明Rt△ABC∽Rt△ACE，从而利用相似比计算PB的长．

解：（1）证明：连接OC，如图，

∵PE是⊙O的切线，

∴OC⊥PE，

∵AE⊥PE，

∴OC∥AE，

∴∠DAC=∠OCA，

∵OA=OC，

∴∠OCA=∠OAC，

∴∠DAC=∠OAC，

∴AC平分∠BAD；

（2）∵AB是⊙O的直径，

∴∠ACB=90°

在Rt△ABC中，BC===1，

在Rt△ABC和Rt△ACE中，

∵∠DAC=∠OAC，∠AEC=∠ACB=90°，

∴Rt△ABC∽Rt△ACE，

∴AC：AB=EC：BC，即2：3=EC：1，

∴EC=；

在Rt△ACE中，AE===，

又∵OC∥AE，

∴Rt△ABC∽Rt△ACE，

∴OC：AE=PO：PA，即：=（PB+）：（PB+3），

∴PB=．