题目内容
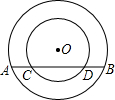
如图所示，同心圆中，大圆的弦AB交小圆于C，D两点，试证明：AC=BD．
【答案】分析：过圆心O作弦的垂线OE，根据垂径定理，OE平分AB和CD，可以说明AC=BD．
解答：
解：如图：过O作OE⊥AB，
由垂径定理可知：OE平分AB，OE平分CD，
∴AE=BE，CE=DE，
∴AE-CE=BE-DE，即AC=BD．
点评：本题考查的是垂径定理，根据题意过圆心作弦的垂线，由垂径定理有：AE=BE，CE=DE，然后把这两个等式相减得到AC=BD．
解答：
解：如图：过O作OE⊥AB，由垂径定理可知：OE平分AB，OE平分CD，
∴AE=BE，CE=DE，
∴AE-CE=BE-DE，即AC=BD．
点评：本题考查的是垂径定理，根据题意过圆心作弦的垂线，由垂径定理有：AE=BE，CE=DE，然后把这两个等式相减得到AC=BD．
练习册系列答案
相关题目
如图所示，同心圆中，大圆的弦AB交小圆于C，D两点，试证明：AC=BD．
如图所示，同心圆中，大圆的弦AB交小圆于C、D两点，且AC=CD，AB的弦心距等于CD的一半．则这两个同心圆的大小圆的半径之比（ ）
如图所示，同心圆中，大圆的弦AB交小圆于C，D两点，试证明：AC=BD．