题目内容
如图所示,同心圆中,大圆的弦AB交小圆于C、D两点,且AC=CD,AB的弦心距等于CD的一半.则这两个同心圆的大小圆的半径之比( )

| A.3:1 | B.2:
| C.10:
| D.
|


过O作OE⊥AB,交AB于点E,连接OA,OC,如图所示,
由垂径定理得到E为AB的中点,E为CD的中点,
又AB的弦心距等于CD的一半,即OE=CE=ED=
| 1 |
| 2 |
∴△OCE为等腰直角三角形,
设CE=OE=x,由勾股定理得到OC=
| 2 |
由AC=CD=2CE,得到AC=2x,
则AE=AC+CE=2x+x=3x,
在Rt△AEO中,根据勾股定理得:OA=
| AE2+OE2 |
| 10 |
则这两个同心圆的大小圆的半径之比OA:OC=
| 10 |
| 2 |
| 5 |
故选D

练习册系列答案
相关题目
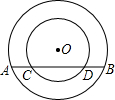 如图所示,同心圆中,大圆的弦AB交小圆于C,D两点,试证明:AC=BD.
如图所示,同心圆中,大圆的弦AB交小圆于C,D两点,试证明:AC=BD. 如图所示,同心圆中,大圆的弦AB交小圆于C、D两点,且AC=CD,AB的弦心距等于CD的一半.则这两个同心圆的大小圆的半径之比( )
如图所示,同心圆中,大圆的弦AB交小圆于C、D两点,且AC=CD,AB的弦心距等于CD的一半.则这两个同心圆的大小圆的半径之比( ) 如图所示,同心圆中,大圆的弦AB交小圆于C,D两点,试证明:AC=BD.
如图所示,同心圆中,大圆的弦AB交小圆于C,D两点,试证明:AC=BD.