题目内容
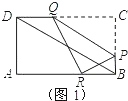
【题目】如图,在矩形ABCD中,AB=9,AD=3![]() ,点P是边BC上的动点(点P不与点B,点C重合),过点P作直线PQ∥BD,交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点,设CP的长度为x,△PQR与矩形ABCD重叠部分的面积为y.
,点P是边BC上的动点(点P不与点B,点C重合),过点P作直线PQ∥BD,交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点,设CP的长度为x,△PQR与矩形ABCD重叠部分的面积为y.
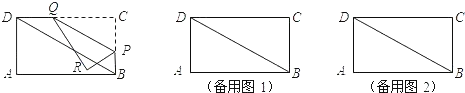
(1)求∠CQP的度数;
(2)当x取何值时,点R落在矩形ABCD的AB边上;
(3)①求y与x之间的函数关系式;
②当x取何值时,重叠部分的面积等于矩形面积的![]() .
.
【答案】(1)∠CQP=30°;(2)x=2![]() ;(3)①
;(3)①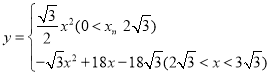 ,②
,②![]()
【解析】
(1)由于PQ与BD平行,∠CQP=∠CDB,因此只需求出∠CDB的度数即可.可在直角三角形ABD中,根据AB,AD的长求出∠ABD的度数,由∠CQP=∠CDB=∠ABD即可得出∠CQP的度数;
(2)当R在AB上时,三角形PBR为直角三角形,且∠BPR=60°(可由(1)的结论得出),根据折叠的性质PR=CP=x,然后用x表示出BP的长,在直角三角形可根据∠RPB的余弦值得出关于x的方程即可求出x的值;
(3)①要分两种情况进行讨论:
一、当R在AB或矩形ABCD的内部时,重合部分是三角形PQR,那么重合部分的面积可通过求三角形CQP的面积来得出,在直角三角形CQP中,已知了∠CQP的度数,可用CP即x的值表示出CQ的长,然后根据三角形的面积计算公式可得出y,x的函数关系式;
二、当R在矩形ABCD的外部时,重合部分是个四边形的面积,如果设RQ,RP与AB的交点分别为E、F,那么重合部分就是四边形EFPQ,它的面积=△CQR的面积﹣△REF的面积.△CQR的面积在一已经得出,关键是求△REF的面积,首先要求出的是两条直角边RE,RF的表达式,可在直角三角形PBF中用一的方法求PF的长,即可通过RP﹣PF得出RF的长;在直角三角形REF中,∠RFE=∠PFB=30°,可用其正切值表示出RE的长,然后可通过三角形的面积计算公式得出三角形REF的面积.进而得出S与x的函数关系式;
②可将矩形的面积代入①的函数式中,求出x的值,然后根据自变量的取值范围来判定求出的x的值是否符合题意.
解:(1)如图,∵四边形ABCD是矩形,
∴AB=CD,AD=BC.
又AB=9,AD=3![]() ,∠C=90°,
,∠C=90°,
∴CD=9,BC=3![]() .
.
∴tan∠CDB=![]() ,
,
∴∠CDB=30°.
∵PQ∥BD,
∴∠CQP=∠CDB=30°;
(2)如图1,由轴对称的性质可知,△RPQ≌△CPQ,
∴∠RPQ=∠CPQ,RP=CP.
由(1)知∠CQP=30°,
∴∠RPQ=∠CPQ=60°,
∴∠RPB=60°,
∴RP=2BP.
∵CP=x,
∴PR=x,PB=3![]() ﹣x.
﹣x.
在△RPB中,根据题意得:2(3![]() ﹣x)=x,
﹣x)=x,
解这个方程得:x=2![]() ;
;
(3)①当点R在矩形ABCD的内部或AB边上时,
![]() ,
,![]() ,
,
∵△RPQ≌△CPQ,
∴当![]() 时,
时,![]()
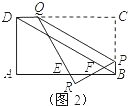
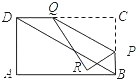
当R在矩形ABCD的外部时(如图2),![]() ,
,
在Rt△PFB中,
∵∠RPB=60°,
∴PF=2BP=2(![]() ﹣x),
﹣x),
又∵RP=CP=x,
∴RF=RP﹣PF=3x﹣6![]() ,
,
在Rt△ERF中,
∵∠EFR=∠PFB=30°,
∴ER=![]() x﹣6.
x﹣6.
∴S△ERF=![]() ER×FR=
ER×FR=![]() x2﹣18x+18
x2﹣18x+18![]() ,
,
∵y=S△RPQ﹣S△ERF,
∴当![]() 时,y=-
时,y=-![]() x2+18x﹣18
x2+18x﹣18![]() .
.
综上所述,y与x之间的函数解析式是: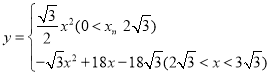 .
.
②矩形面积=![]() ,
,
当![]() 时,函数
时,函数![]() 随自变量的增大而增大,
随自变量的增大而增大,
所以y的最大值是6![]() ,而矩形面积的
,而矩形面积的![]() 的值=
的值=![]() ,
,
而![]() ,所以,当
,所以,当![]() 时,y的值不可能是矩形面积的
时,y的值不可能是矩形面积的![]() ;
;
当![]() 时,根据题意,得:
时,根据题意,得:![]() ,
,
解这个方程,得![]() ,
,
因为![]() ,
,
所以![]() 不合题意,舍去.
不合题意,舍去.
所以![]() .
.
综上所述,当![]() 时,△PQR与矩形ABCD重叠部分的面积等于矩形面积的
时,△PQR与矩形ABCD重叠部分的面积等于矩形面积的![]() .
.

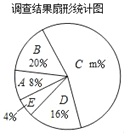
【题目】勤俭节约一直是中华民族的传统美德,某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛,为此先对同学们每月零花钱的数额进行一些了解,随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | a |
C | 60≤x<90 | b |
D | 90≤x<120 | 8 |
E | 120≤x<150 | 2 |
根据以上图表,解答下列问题:
(1)填空:这次调查的同学共有 人,a+b= ,m= ;
(2)求扇形统计图中扇形B的圆心角的度数;
(3)该校共有1200名学生,请估计每月零花钱的数额在60≤x<90范围的人数.