Question

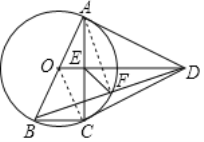
【题目】如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接 AC、OD交于点E．

(1)若tan∠ABC=2，证明：DA与⊙O相切：

(2)在(1)条件下，连接BD交⊙O于点F，连接EF，若BC=1，求EF的长．

Answer 1

【答案】(1)证明见解析；（2）EF=

【解析】

（1）连接OC，证△OAD≌△OCD得∠ADO=∠CDO，由AD=CD知DE⊥AC，再由AB为直径知BC⊥AC，从而证明OD∥BC；再根据tan∠ABC=2可设BC=a、则AC=2a、AD=AB=，证OE为中位线知OE=a、AE=CE=AC=a，进一步求得DE=，再在△AOD中利用勾股定理逆定理证∠OAD=90°即可得；

（2）先证△AFD∽△BAD得DFBD=AD2 ①，再证△AED∽△OAD得ODDE=AD2 ②，由①②得DFBD=ODDE，即，结合∠EDF=∠BDO知△EDF∽△BDO，据此可得，结合（1）可得相关线段的长，代入计算可得．

解：（1）连接OC，

在△OAD和△OCD中，

，

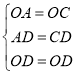∴△OAD≌△OCD（SSS），
∴∠ADO=∠CDO，
又AD=CD，
∴DE⊥AC，
∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠ACB=90°，即BC⊥AC，
∴OD∥BC，

∵tan∠ABC=，

∴设BC=a、则AC=2a，
∴AD=AB=，

∵OE∥BC，且AO=BO，
∴OE=BC=a，AE=CE=AC=a，

在△AED中，DE=，

在△AOD中，AO2+AD2=（）2+（）2=，

OD2=（OE+DE）2=（a+2a）2=，

∴AO2+AD2=OD2，
∴∠OAD=90°，
则DA与⊙O相切；

（2）连接AF，
∵AB是⊙O的直径，
∴∠AFD=∠BAD=90°，
∵∠ADF=∠BDA，
∴△AFD∽△BAD，
∴，即DFBD=AD2 ①，
又∵∠AED=∠OAD=90°，∠ADE=∠ODA，
∴△AED∽△OAD，
∴，即ODDE=AD2 ②，
由①②可得DFBD=ODDE，即，

又∵∠EDF=∠BDO，
∴△EDF∽△BDO，
∵BC=1，
∴AB=AD=，OD=，ED=2，BD=，OB=，

∴，即，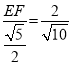

解得：EF=.