题目内容
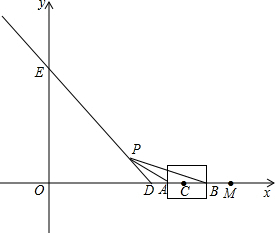 如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,
如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心,t个单位长度为边长的正方形(两边与y轴平行)与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当正方形与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
分析:(1)根据题意,得t秒时,点C的横坐标为5-t,纵坐标为0;由于动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.
(2)①当点A到达点D时,所用的时间是t的最小值,此时DC=OC-OD=5-t-3=
t,得到t≥
;当正方形在点D左侧且右上边顶点交于DE时,为t的最大值,如图,易得Rt△CDF∽Rt△EDO,有
=
,求解得到t的最大值.
②当△PAB为等腰三角形时,有三种情况:PA=AB,PA=PB,PB=AB.根据勾股定理,求得每种情况的t的值.
(2)①当点A到达点D时,所用的时间是t的最小值,此时DC=OC-OD=5-t-3=
| 1 |
| 2 |
| 4 |
| 3 |
| CF |
| 4 |
| 3-(5-t) |
| 5 |
②当△PAB为等腰三角形时,有三种情况:PA=AB,PA=PB,PB=AB.根据勾股定理,求得每种情况的t的值.
解答: 解:(1)如图1,过点P作PQ⊥x轴于点Q,
解:(1)如图1,过点P作PQ⊥x轴于点Q,
当t秒时,有PD=t,DE=5,OE=4,OD=3,
则PQ:EO=DQ:OD=PD:ED,
∴PQ=
t,DQ=
t.
∴C(5-t,0),P(3-
t,
t).
(2)
①当正方形中心C由点M(5,0)向左运动,使点A到点D并随正方形继续向左运动时,
有DC=OC-OD=5-t-3=
t,
即5-
t≤3,
解得:t≥
.
当点C在点D左侧时,如图2,过点C作CF⊥射线DE,垂足为F,
则由∠CDF=∠EDO,
得△CDF∽△EDO,
则
=
,
解得CF=
.

由图3可得出:CF<OQ=
t,
即
<
t,
解得t<
.
∴当⊙C与射线DE有公共点时,
t的取值范围为
≤t<
.

②如图4,当PA=AB时,过P作PQ⊥x轴,垂足为Q.
有PA2=PQ2+AQ2=
t 2+(5-
t-3+
t)2.
则
t2-
t+4=t2,
即9t2-72t+80=0,
解得t1=
,t2=
.

如图5,当PA=PB时有PC⊥AB,
则5-t=3-
t,
解得t3=5;

如图6,当PB=AB时,有
PB 2=PQ 2+BQ 2=
t2+(5-
t-3+
t)2,
则
t2+
t+4=t2,
即7t2-8t-80=0,
解得t4=4,t5=-
(不合题意,舍去),
故当△PAB是等腰三角形时,t=
,或t=4,或t=5,或t=
,
又因为C是从M点向左运动的,
故t=
或t=4或t=5或t=
,

 解:(1)如图1,过点P作PQ⊥x轴于点Q,
解:(1)如图1,过点P作PQ⊥x轴于点Q,当t秒时,有PD=t,DE=5,OE=4,OD=3,
则PQ:EO=DQ:OD=PD:ED,
∴PQ=
| 4 |
| 5 |
| 3 |
| 5 |
∴C(5-t,0),P(3-
| 3 |
| 5 |
| 4 |
| 5 |
(2)
①当正方形中心C由点M(5,0)向左运动,使点A到点D并随正方形继续向左运动时,
有DC=OC-OD=5-t-3=
| 1 |
| 2 |
即5-
| 3 |
| 2 |
解得:t≥
| 4 |
| 3 |
当点C在点D左侧时,如图2,过点C作CF⊥射线DE,垂足为F,
则由∠CDF=∠EDO,
得△CDF∽△EDO,
则
| CF |
| 4 |
| 3-(5-t) |
| 5 |
解得CF=
| 4t-8 |
| 5 |

由图3可得出:CF<OQ=
| ||
| 2 |
即
| 4t-8 |
| 5 |
| ||
| 2 |
解得t<
64+40
| ||
| 7 |
∴当⊙C与射线DE有公共点时,
t的取值范围为
| 4 |
| 3 |
64+40
| ||
| 7 |

②如图4,当PA=AB时,过P作PQ⊥x轴,垂足为Q.
有PA2=PQ2+AQ2=
| 16 |
| 25 |
| 3 |
| 2 |
| 3 |
| 5 |
则
| 29 |
| 20 |
| 18 |
| 5 |
即9t2-72t+80=0,
解得t1=
| 4 |
| 3 |
| 20 |
| 3 |

如图5,当PA=PB时有PC⊥AB,
则5-t=3-
| 3 |
| 5 |
解得t3=5;

如图6,当PB=AB时,有
PB 2=PQ 2+BQ 2=
| 16 |
| 25 |
| 1 |
| 2 |
| 3 |
| 5 |
则
| 13 |
| 20 |
| 2 |
| 5 |
即7t2-8t-80=0,
解得t4=4,t5=-
| 20 |
| 7 |
故当△PAB是等腰三角形时,t=
| 4 |
| 3 |
| 20 |
| 3 |
又因为C是从M点向左运动的,
故t=
| 4 |
| 3 |
| 20 |
| 3 |

点评:此题主要考查了相似三角形和方程不等式、正方形等方面的知识.重点考查学生是否认真审题,挖掘出题中的隐含条件,综合运用数学知识解决实际问题的能力,以及运用转化的思想,方程的思想,数形结合的思想和分类讨论的思想解决实际问题的能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
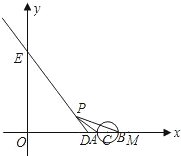 以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒.
以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒. 交于A、B两点(点A在点B的左侧).
交于A、B两点(点A在点B的左侧).
 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.