题目内容
如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,设运动时间为t秒,以点C为圆心、
t个单位长度为半径的⊙C与x轴 交于A、B两点(点A在点B的左侧).
交于A、B两点(点A在点B的左侧).
(1)请用含t的代数式分别表示出点A、B、C的坐标;
(2)①当⊙C恰好经过D点时,求t的值;
②当⊙C与射线DE相切时,求t的值;
(3)直接写出当⊙C与射线DE有公共点时t的取值范围.
| 1 | 2 |
 交于A、B两点(点A在点B的左侧).
交于A、B两点(点A在点B的左侧).(1)请用含t的代数式分别表示出点A、B、C的坐标;
(2)①当⊙C恰好经过D点时,求t的值;
②当⊙C与射线DE相切时,求t的值;
(3)直接写出当⊙C与射线DE有公共点时t的取值范围.
分析:(1)根据CM=t,CO-AC=OM-CM-AC=5-t-
t=5-
t,进而得出A,B,C点坐标即可;
(2)①当⊙C恰好经过D点时,点A或点B与D重合,进而得出等式方程求出即可;
②由图可知,当点C在点D左侧时,⊙C才能与射线DE相切,过点C作CF⊥射线DE,垂足为F,得△CDF∽△EDO,求出t的值即可;
(3)当点A到达点D时,所用的时间是t的最小值,此时DC=OC-OD=5-t-3=
t,得到t≥
,当圆C在点D左侧且与ED相切时,为t的最大值,即可得出t的取值范围.
| 1 |
| 2 |
| 3 |
| 2 |
(2)①当⊙C恰好经过D点时,点A或点B与D重合,进而得出等式方程求出即可;
②由图可知,当点C在点D左侧时,⊙C才能与射线DE相切,过点C作CF⊥射线DE,垂足为F,得△CDF∽△EDO,求出t的值即可;
(3)当点A到达点D时,所用的时间是t的最小值,此时DC=OC-OD=5-t-3=
| 1 |
| 2 |
| 4 |
| 3 |
解答: 解:(1)根据点C从M点向左移动,
解:(1)根据点C从M点向左移动,
则CM=t,CO-AC=OM-CM-AC=5-t-
t=5-
t,
BO=5-
t+t=5-
t,
故A(5-
t,0)、B(5-
t,0)、C(5-t,0).
(2)①当⊙C恰好经过D点时,点A或点B与D重合,
∴5-
t=3或5-
t=3,解得t=
或t=4,
∴当⊙C恰好经过D点时t的值为
或4.
②由图可知,当点C在点D左侧时,⊙C才能与射线DE相切,过点C作CF⊥射线DE,垂足为F,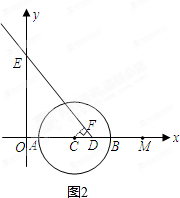
则由∠CDF=∠EDO,得△CDF∽△EDO,
则
=
.解得CF=
.
∵⊙C与射线DE相切,∴CF=
t,即
=
t,解得t=
.
∴当⊙C与射线DE相切时,t的值为
;
(3)当⊙C的圆心C由点M(5,0)向左运动,使点A到点D并随⊙C继续向左运动时,
有5-
t≤3,即t≥
.
利用(2)中CF=
,
由CF≤
t,即
≤
t,解得t≤
.
∴当⊙C与射线DE有公共点时,t的取值范围为
≤t≤
.
 解:(1)根据点C从M点向左移动,
解:(1)根据点C从M点向左移动,则CM=t,CO-AC=OM-CM-AC=5-t-
| 1 |
| 2 |
| 3 |
| 2 |
BO=5-
| 3 |
| 2 |
| 1 |
| 2 |
故A(5-
| 3 |
| 2 |
| 1 |
| 2 |
(2)①当⊙C恰好经过D点时,点A或点B与D重合,
∴5-
| 3 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
∴当⊙C恰好经过D点时t的值为
| 4 |
| 3 |
②由图可知,当点C在点D左侧时,⊙C才能与射线DE相切,过点C作CF⊥射线DE,垂足为F,

则由∠CDF=∠EDO,得△CDF∽△EDO,
则
| CF |
| 4 |
| 3-(5-t) |
| 5 |
| 4t-8 |
| 5 |
∵⊙C与射线DE相切,∴CF=
| 1 |
| 2 |
| 4t-8 |
| 5 |
| 1 |
| 2 |
| 16 |
| 3 |
∴当⊙C与射线DE相切时,t的值为
| 16 |
| 3 |
(3)当⊙C的圆心C由点M(5,0)向左运动,使点A到点D并随⊙C继续向左运动时,
有5-
| 3 |
| 2 |
| 4 |
| 3 |
利用(2)中CF=
| 4t-8 |
| 5 |
由CF≤
| 1 |
| 2 |
| 4t-8 |
| 5 |
| 1 |
| 2 |
| 16 |
| 3 |
∴当⊙C与射线DE有公共点时,t的取值范围为
| 4 |
| 3 |
| 16 |
| 3 |
点评:本题为代数与几何有一定难度的综合题,它综合考查了用变量t表示点的坐标,直线(射线)与圆的位置关系,相似三角形和方程不等式等方面的知识.重点考查学生是否认真审题,挖掘出题中的隐含条件,综合运用数学知识解决实际问题的能力,以及运用转化的思想,方程的思想,数形结合的思想和分类讨论的思想解决实际问题的能力.

练习册系列答案
相关题目
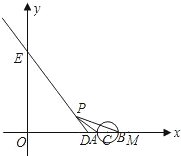 以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒.
以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒.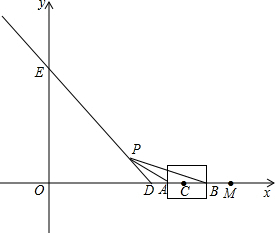 如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,
如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,
 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.