题目内容
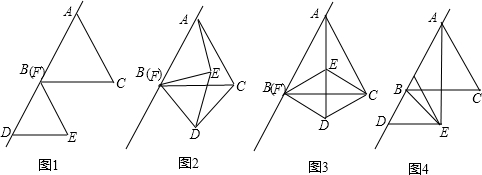
如图，将正△ABC沿过点A的直线l翻折得到△ADE，连接BD，CD，则∠BDC=
- A.30°
- B.60°
- C.25°
- D.15°
A
分析：利用折叠易得∠CBD=∠BDE，由AC=AD得∠ACD=∠ADC，由△BCD的内角和即可求得所求角的度数．
解答：根据题意得∠CBD=∠BDE，AC=AD
∴∠ACD=∠ADC，
∵∠BCA=∠ADE=60°，
∴∠CBD+∠ACD+∠BDC=120°
∴∠ADB+∠BDC+∠BDC+∠BDC+∠CDE=120°
又∵∠ADB+∠BDC+∠CDE=60°
∴2∠BDC=60°
∴∠BDC=30°．
故选A．
点评：本题综合考查折叠前后对应角相等，等边三角形的性质，等边对等角等知识点．
分析：利用折叠易得∠CBD=∠BDE，由AC=AD得∠ACD=∠ADC，由△BCD的内角和即可求得所求角的度数．
解答：根据题意得∠CBD=∠BDE，AC=AD
∴∠ACD=∠ADC，
∵∠BCA=∠ADE=60°，
∴∠CBD+∠ACD+∠BDC=120°
∴∠ADB+∠BDC+∠BDC+∠BDC+∠CDE=120°
又∵∠ADB+∠BDC+∠CDE=60°
∴2∠BDC=60°
∴∠BDC=30°．
故选A．
点评：本题综合考查折叠前后对应角相等，等边三角形的性质，等边对等角等知识点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7、如图，将正△ABC沿过点A的直线L翻折得到△ADE，连接BD，CD，则∠BDC=（ ）
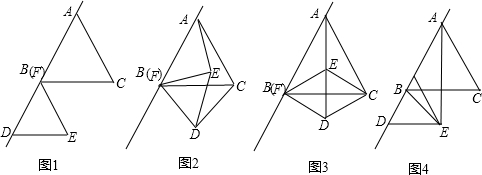
，把图1中的△FDE绕点B逆时针方向旋转90°（如图3），试判断四边形EBDC的形状，并说明你的理由；
