题目内容
某中学生暑期社会调查团共17人到几个地方去考察,事先预算住宿费平均每人每天不超过x元.一日到达某地,该地有两处招待所A,B.A有甲级床位8个,乙级床位11个;B有甲级床位10个,乙级床位4个,丙级床位6个.已知甲,乙,丙床位每天分别为14元,8元,5元.若全团集中住在一个招待所里,按预算只能住B处,则整数x=________.
10
分析:关系式为:17x<A招待所最低的住宿费用,17x≥B招待所最低的住宿费用,把相关数值代入计算即可.
解答:在A招待所17个人的最低住宿方案为住乙级床位11个,甲级床位6个,住宿费用为:11×8+6×14=172元.
在B招待所17个人的最低住宿方案为住丙级床位6个,乙级床位4个,甲级床位7个.住宿费用为:5×6+8×4+14×7=160元,
∴ ,
,
解得9 ≤x<10
≤x<10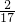 ,
,
∵x为整数,
∴x为10,
故答案为10.
点评:本题考查了一元一次不等式组的应用,得到在两个招待所的最低住宿费是解决本题的突破点,得到预算总住宿费的2个关系式是解决本题的关键.
分析:关系式为:17x<A招待所最低的住宿费用,17x≥B招待所最低的住宿费用,把相关数值代入计算即可.
解答:在A招待所17个人的最低住宿方案为住乙级床位11个,甲级床位6个,住宿费用为:11×8+6×14=172元.
在B招待所17个人的最低住宿方案为住丙级床位6个,乙级床位4个,甲级床位7个.住宿费用为:5×6+8×4+14×7=160元,
∴
 ,
,解得9
 ≤x<10
≤x<10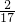 ,
,∵x为整数,
∴x为10,
故答案为10.
点评:本题考查了一元一次不等式组的应用,得到在两个招待所的最低住宿费是解决本题的突破点,得到预算总住宿费的2个关系式是解决本题的关键.

练习册系列答案
相关题目
某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9.利用上述数据估计该小区2000户家庭一周内需要环保方便袋约( )
| A、2000只 | B、14000只 | C、21000只 | D、98000只 |