题目内容
如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
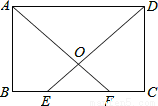
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,然后求出BF=CE,再利用“边角边”证明△ABF和△DCE全等即可;
(2)根据全等三角形对应角相等可得∠BAF=∠EDC,然后求出∠DAF=∠EDA,然后根据等腰三角形的定义证明即可.
试题解析:(1)在矩形ABCD中,∠B=∠C=90°,AB=DC,
∵BE=CF,BF=BC-FC,CE=BC-BE,
∴BF=CE,
在△ABF和△DCE中,
 ,
,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠BAF=∠EDC,
∵∠DAF=90°-∠BAF,∠EDA=90°-∠EDC,
∴∠DAF=∠EDA,
∴△AOD是等腰三角形.
考点:1.矩形的性质;2.全等三角形的判定与性质;3.等腰三角形的判定.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ,其中
,其中
 是关于的一元二次方程
是关于的一元二次方程 的两个根,那么
的两个根,那么 的值是( )
的值是( ) B.4 C.
B.4 C. D.2
D.2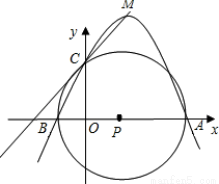
 与⊙O相交于A、B两点,M、N 是 ⊙O上的两个动点,且在直线
与⊙O相交于A、B两点,M、N 是 ⊙O上的两个动点,且在直线 ,则四边形MANB面积的最大值是 。
,则四边形MANB面积的最大值是 。

