题目内容
已知关于x的一元二次方程x2-(m+6)x+3m+9=0的两个实数根分别为x1,x2.
(1)求证:该一元二次方程总有两个实数根;
(2)若n=x1+x2-5,判断动点P(m,n)所形成的函数图象是否经过点A(4,5),并说明理由.
(1)求证:该一元二次方程总有两个实数根;
(2)若n=x1+x2-5,判断动点P(m,n)所形成的函数图象是否经过点A(4,5),并说明理由.
考点:根的判别式,根与系数的关系
专题:
分析:(1)先求出该一元二次方程的△的值,再根据一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根即可得出答案.
(2)根据x1+x2=-
和n=x1+x2-5,表示出n,再把点A(4,5)代入,即可得出答案.
(2)根据x1+x2=-
| b |
| a |
解答:解:(1)∵△=(m+6)2-4(3m+9)=m2+12m+36-12m-36=m2≥0,
∴该一元二次方程总有两个实数根;
(2)动点P(m,n)所形成的函数图象经过点A(4,5);
理由:
∵x1+x2=m+6,n=x1+x2-5,
∴n=m+1,
∵当m=4时,n=5,
∴动点P(m,n)所形成的函数图象经过点A(4,5).
∴该一元二次方程总有两个实数根;
(2)动点P(m,n)所形成的函数图象经过点A(4,5);
理由:
∵x1+x2=m+6,n=x1+x2-5,
∴n=m+1,
∵当m=4时,n=5,
∴动点P(m,n)所形成的函数图象经过点A(4,5).
点评:本题考查了根的判别式、根与系数的关系,解题的关键是掌握根的判别式、根与系数的关系的表达式;一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.

练习册系列答案
相关题目
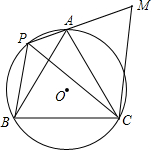 如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与A、B重合),连AP,BP,过C作CM∥BP交PA的延长线于点M,
如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与A、B重合),连AP,BP,过C作CM∥BP交PA的延长线于点M, 如图,在等边三角形△ABC中,射线AD四等分∠BAC交BC于点D,其中∠BAD>∠CAD,则
如图,在等边三角形△ABC中,射线AD四等分∠BAC交BC于点D,其中∠BAD>∠CAD,则