题目内容
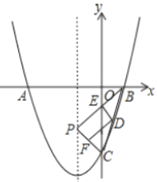
【题目】已知,如图抛物线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() ,
,![]() ,
,![]() ,点P是线段AB上方的抛物线上的一个动点.
,点P是线段AB上方的抛物线上的一个动点.
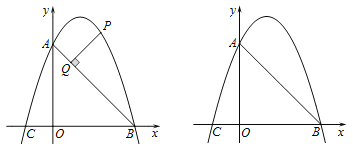
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 过点P作
过点P作![]() 于点Q,当线段PQ的长度最大时,求点P的坐标,和PQ最大值;
于点Q,当线段PQ的长度最大时,求点P的坐标,和PQ最大值;
![]() 过点P作x轴的垂线交线段AB于点M,再过点P作
过点P作x轴的垂线交线段AB于点M,再过点P作![]() 轴交抛物线于点N,请问是否存在点P使
轴交抛物线于点N,请问是否存在点P使![]() 为等腰直角三角形?若存在,求点P的坐标;若不存在说明理由.
为等腰直角三角形?若存在,求点P的坐标;若不存在说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 最大值为
最大值为![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据题意利用待定系数法将点![]() 、
、![]() 代入抛物线的顶点式即可求出;
代入抛物线的顶点式即可求出;
(2)由题意过点P作![]() 与点M,交AB于点N,作
与点M,交AB于点N,作![]() 于点G,并设直线AB解析式为
于点G,并设直线AB解析式为![]() 与求出解析式,进而设
与求出解析式,进而设![]() 其中
其中![]() ,则
,则![]() ,建立关系式并运用配方法求得点P的坐标和PQ最大值;
,建立关系式并运用配方法求得点P的坐标和PQ最大值;
(3)根据题意可知若△PDE为等腰直角三角形,则PD=PE,设点P的横坐标为a,表示出PD、PE的长,列出关于a的方程,解之可得答案.
解:![]() 抛物线过点
抛物线过点![]() 、
、![]() ,
,
![]() 设抛物线解析式为
设抛物线解析式为![]() ,
,
将点![]() 代入,得:
代入,得:![]() ,
,
解得:![]() ,
,
所以抛物线解析式为![]() ;
;
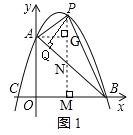
![]() 如图1,过点P作
如图1,过点P作![]() 与点M,交AB于点N,作
与点M,交AB于点N,作![]() 于点G,
于点G,
设直线AB解析式为![]() ,
,
将点![]() 、
、![]() 代入,得:
代入,得:
![]()
解得:![]()
则直线AB解析式为![]() ,
,
设![]() 其中
其中![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() 当
当![]() 时,点P的坐标为
时,点P的坐标为![]() ,
,![]() 的面积有最大值,最大值为
的面积有最大值,最大值为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
解得:![]() ,
,
![]() 最大值为
最大值为![]() ;
;
![]() 如图2,
如图2,
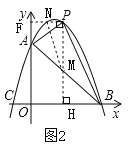
若![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() ,
,
设点P的横坐标为a,点N的横坐标为b,
![]() ,
,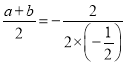 ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() 或
或![]() ,
,
所以![]() 或
或![]() .
.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 | 12 |
y | 12 | 6 | ■ | 3 | 2 | 1.5 | 1 | 0.5 |
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形![]() 的面积记为
的面积记为![]() ,矩形
,矩形![]() 的面积记为
的面积记为![]() ,请判断
,请判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
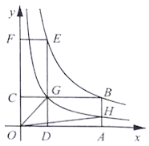
(4)在(3)的条件下,![]() 交
交![]() 于点G,反比例函数
于点G,反比例函数![]() 的图象经过点G交
的图象经过点G交![]() 于点H,连接
于点H,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为_________.
的面积为_________.
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.