题目内容
16.如图,在数轴上A表示的数为a,B点表示的数为b,且a、b满足|a-6|+(b+$\frac{2}{3}$a)2=0.若动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,动点P在动点Q运动2秒后从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,动点P运动9秒,P、Q两点重合.
分析 根据非负数的性质求出a=6,b=-4,再根据两点间的距离公式求出AB=6-(-4)=10,追击问题的相等关系列出方程于是得到结论.
解答 解:∵|a-6|+(b+$\frac{2}{3}$a)2=0,
∴a-6=0,b+$\frac{2}{3}$a=0,
∴a=6,b=-4,
∴AB=6-(-4)=10;
动点Q沿数轴向左匀速运动,由题意得
6t-4(t+2)=10,解得t=9.
故动点P运动9秒,P、Q两点重合,
故答案为:9.
点评 本题考查了一元一次方程的应用,数轴,两点间的距离,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
6.如图,某乡镇第一季度“家电下乡”产品的购买情况绘制成的两幅不完整的统计图,请根据统计图提供的信息解答下列问题:
(1)求第一季度购买的“家电下乡”产品的总台数;
(2)通过计算,把两幅统计图补充完整.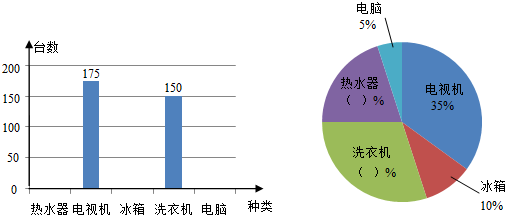
(1)求第一季度购买的“家电下乡”产品的总台数;
(2)通过计算,把两幅统计图补充完整.

7. 如图,AD垂直平分线段BC,垂足为D,∠ABC的平分线BE交AD于点E,连接EC,若∠ABC=50°,则∠C的度数是( )
如图,AD垂直平分线段BC,垂足为D,∠ABC的平分线BE交AD于点E,连接EC,若∠ABC=50°,则∠C的度数是( )
 如图,AD垂直平分线段BC,垂足为D,∠ABC的平分线BE交AD于点E,连接EC,若∠ABC=50°,则∠C的度数是( )
如图,AD垂直平分线段BC,垂足为D,∠ABC的平分线BE交AD于点E,连接EC,若∠ABC=50°,则∠C的度数是( )| A. | 25° | B. | 20° | C. | 50° | D. | 65° |
4.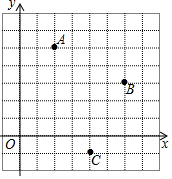 如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
 如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
如图,点A,B,C的坐标分别为(2,5),(6,3),(4,-1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )| A. | (0,0) | B. | (0,1) | C. | (3,2) | D. | (1,0) |
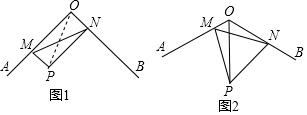
11. 如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )
如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )
 如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )
如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
1.下列说法正确的是( )
| A. | a和0是都是单项式 | B. | 多项式-3a2b+7a2b2的次数是3 | ||
| C. | 单项式$-\frac{2}{3}{a^2}b$的系数为-2 | D. | ${x^2}+\frac{2}{y}$是整式 |