题目内容
某商品在最近的100天内的价格F与时间t(天)的函数关系是F= ,其中t是非负数.
,其中t是非负数.
销售量G与时间t的函数关系是G=- t+
t+ ,0≤t≤100,其中t是非负数.求这种商品的日销售额的最大值.
,0≤t≤100,其中t是非负数.求这种商品的日销售额的最大值.
解:设日销售额为y,则y=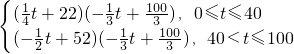 ,
,
当0≤t≤40时,y=- t2+t+
t2+t+ =-
=- (t-6)2+3+
(t-6)2+3+ ,当t=6时,最大值为:
,当t=6时,最大值为: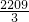 .
.
当40<t≤100时,y= t2-34t+
t2-34t+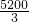 =
= (t-102)2-
(t-102)2-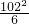 +
+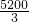 ,当t=41时,y取得最大值为:
,当t=41时,y取得最大值为: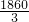 ,
,
综上所述:当t=6时,这种商品的日销售额的最大值为: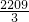 .
.
分析:设日销售额为y,则y等于价格F乘以销售量G,用配方法即可求出日销售额的最大值.
点评:本题考查了二次函数的最值,难度一般,关键是根据分段函数不同的解析式用配方法进行求解.
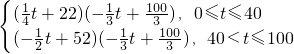 ,
,当0≤t≤40时,y=-
 t2+t+
t2+t+ =-
=- (t-6)2+3+
(t-6)2+3+ ,当t=6时,最大值为:
,当t=6时,最大值为: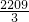 .
.当40<t≤100时,y=
 t2-34t+
t2-34t+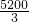 =
= (t-102)2-
(t-102)2-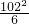 +
+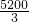 ,当t=41时,y取得最大值为:
,当t=41时,y取得最大值为: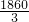 ,
,综上所述:当t=6时,这种商品的日销售额的最大值为:
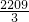 .
.分析:设日销售额为y,则y等于价格F乘以销售量G,用配方法即可求出日销售额的最大值.
点评:本题考查了二次函数的最值,难度一般,关键是根据分段函数不同的解析式用配方法进行求解.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 ,其中t是非负数.
,其中t是非负数. t+
t+ ,0≤t≤100,其中t是非负数.求这种商品的日销售额的最大值.
,0≤t≤100,其中t是非负数.求这种商品的日销售额的最大值.