题目内容
 如图△ABC,∠A=30°,tanB=1,BC=
如图△ABC,∠A=30°,tanB=1,BC= ,则AB=________.
,则AB=________.
2+
分析:过点C作CD⊥AB于D,在直角三角形CDB和直角三角形ADC中利用45°和30°角的三角函数值分别求出AD和BD的长即可.
解答: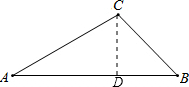 解:过点C作CD⊥AB于D,
解:过点C作CD⊥AB于D,
在直角三角形CDB,∵tanB=1,
∴∠B=45°,
∴CD=BD
∴cos45°= =
= ,
,
∵BC= ,
,
∴BD=2,
∴CD=2,
∵∠A=30°,
∴tanA= =
= ,
,
∴AD=2 ,
,
∴AB=AD+DB=2+2 .
.
故答案为:2+ .
.
点评:此题考查了解直角三角形,以及特殊角的锐角三角函数定义,作出相应的辅助线是本题的突破点.

分析:过点C作CD⊥AB于D,在直角三角形CDB和直角三角形ADC中利用45°和30°角的三角函数值分别求出AD和BD的长即可.
解答:
 解:过点C作CD⊥AB于D,
解:过点C作CD⊥AB于D,在直角三角形CDB,∵tanB=1,
∴∠B=45°,
∴CD=BD
∴cos45°=
 =
= ,
,∵BC=
 ,
,∴BD=2,
∴CD=2,
∵∠A=30°,
∴tanA=
 =
= ,
,∴AD=2
 ,
,∴AB=AD+DB=2+2
 .
.故答案为:2+
 .
.点评:此题考查了解直角三角形,以及特殊角的锐角三角函数定义,作出相应的辅助线是本题的突破点.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线;
已知:如图△ABC中,AB=AC,CD、BE是△ABC的角平分线;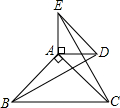 已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.
已知:如图△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.

 (2012•宁津县一模)如图△ABC中BD和CE是两条高,∠A=45°,∠ADE=∠ABC,则
(2012•宁津县一模)如图△ABC中BD和CE是两条高,∠A=45°,∠ADE=∠ABC,则 如图△ABC的面积为a.
如图△ABC的面积为a.