Question

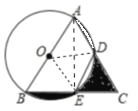
【题目】如图，以△ABC的一边AB为直径作⊙O，交AC，BC于D，E两点，若AB=4，∠BED=120°，点E是BD中点，则图中阴影部分的面积是（　　）

A. 4 B. C. D.

Answer 1

【答案】D

【解析】连接OE、OD、AE．

∵∠BED=120°，

∴∠BAC=60°，

∵，

∴BE=ED，

∵OB=OE=OD，

∴△OEB≌△OED，

∴∠OEB=∠OED=60°，

∴∠ABC=∠BAC=60°，

∴△ABC是等边三角形，

∴AB=BC=AC=4，

∵AB为直径，

∴∠AEB=90°，BE=EC=BC=2，

∵OB=OE，∠ABC=∠BAC=60°，OA=OD，

∴△OBE、△AOD、△ODE、△CDE都是等边三角形，

∴OB=BE=OE=2，OA=OD=AD=2，∠AOD=∠BOE=60°，

∴∠EOD=180°﹣60°﹣60°=60°，

∴阴影部分的面积是=（扇形BOE的面积﹣三角形BOE面积）+（菱形OECD的面积﹣扇形OED的面积）=三角形CDE的面积=×22=.

故选D．