��Ŀ����
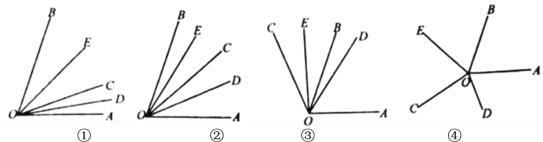
����Ŀ����֪�߶�AB=m(mΪ����)����CΪֱ��AB��һ�㣨�����A��B�غϣ�����M��N�ֱ����߶�BC��AC�ϣ�������CN=3AN��CM=3BM.
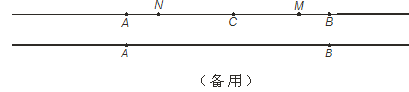
(1)��ͼ������Cǡ�����߶�AB�е㣬��m=8ʱ����MN=______��
(2) ����C�ڵ�A��࣬ͬʱ��M���߶�AB��(����˵��غ�)�����ж�CN+2AM -2MN��ֵ�Ƿ���m�йأ���˵������.
(3) ����C��ֱ��AB��һ�㣨�����A��B�غϣ���ͬʱ��M���߶�AB��(����˵��غ�)����MN���� (�ú�m�Ĵ���ʽ��ʾ).
���𰸡�(1)6��(2) �أ����ɼ�������(3)![]() m.
m.
��������
��1�������е�ɵõ�AC��BC�ij����ٸ���CN=3AN��CM=3BM���ɼ����CN��CM���������߶εĺͲ��ϵ���м��㼴�ɣ�
��2�������߶�֮��Ĺ�ϵ��CN=3AN��CM=3BM���ֱ��ʾ��CN��AM��MN���ٽ��л��ɣ�
��3����������ۣ�����ͼ�Σ������߶�֮��Ĺ�ϵ���㼴��.
�⣺��1���ߵ�Cǡ�����߶�AB�е㣬��AB=m=8��
��AC=BC=![]() AB=4��
AB=4��
��CN=3AN��CM=3BM��
��CN=![]() AC��CM=
AC��CM=![]() BC��
BC��
��CN=3��CM=3��
��MN=CN+CM=3+3=6;
��2����C��A����ߣ���ͼ��ʾ��
![]()
��CN=3AN��CM=3BM��
��MN=CM��CN=3BM��3AN��
��AM=MN��AN=3BM��3AN��AN=3BM��4AN��
��CN +2AM��2MN=3AN+2(3BM��4AN)��2(3BM��3AN)=AN��
��CN +2AM��2MN��ֵ��m�أ�
��3���ٵ���C���߶�AB��ʱ����ͼ��ʾ��
![]()
��CN=3AN��CM=3BM��
��CN=![]() AC��CM=
AC��CM=![]() BC��
BC��
��MN=CM+CN=![]() BC+
BC+![]() AC=
AC=![]() (BC+AC)=
(BC+AC)=![]() AB=
AB=![]() m��
m��
�ڵ���C�ڵ�A����ߣ���ͼ��ʾ��
![]()
��CN=3AN��CM=3BM��
��CN=![]() AC��BM=
AC��BM=![]() BC��
BC��
��MN=BC��CN��BM=BC��![]() AC��
AC��![]() BC =
BC =![]() (BC��AC)=
(BC��AC)=![]() AB=
AB=![]() m��
m��
�۵���C�ڵ�B���ұߣ���ͼ��ʾ��
![]()
��CN=3AN��CM=3BM��
��AN=![]() AC��CM=
AC��CM=![]() BC��
BC��
��MN=AC��AN��CM=AC��![]() AC��
AC��![]() BC =
BC =![]() (AC��BC)=
(AC��BC)=![]() AB=
AB=![]() m��
m��
����������MN�ij���Ϊ![]() m.
m.

 ������������ϵ�д�
������������ϵ�д�