题目内容
【题目】如图,![]() 是一条射线,
是一条射线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线.
的平分线.
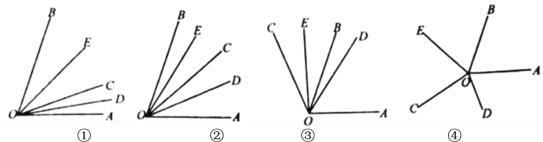
(1)如图①,当![]() 时,则
时,则![]() 的度数为________________;
的度数为________________;
(2)如图②,当射线![]() 在
在![]() 内绕
内绕![]() 点旋转时,
点旋转时,![]() 、
、![]() 、
、![]() 三角之间有怎样的数量关系?并说明理由;
三角之间有怎样的数量关系?并说明理由;
(3)当射线![]() 在
在![]() 外如图③所示位置时,(2)中三个角:
外如图③所示位置时,(2)中三个角:![]() 、
、![]() 、
、![]() 之间数量关系的结论是否还成立?给出结论并说明理由;
之间数量关系的结论是否还成立?给出结论并说明理由;
(4)当射线![]() 在
在![]() 外如图④所示位置时,
外如图④所示位置时,![]() 、
、![]() 、
、![]() 之间数量关系是____________.
之间数量关系是____________.
【答案】(1)![]() ;(2)
;(2)![]() ,详见解析;(3)不成立,
,详见解析;(3)不成立,![]() ,详见解析;(4)
,详见解析;(4)![]() ;
;
【解析】
(1)(2)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() AOB,即可得出答案;(3)根据角平分线定义得出∠DOC=
AOB,即可得出答案;(3)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() (∠AOC∠BOC)=
(∠AOC∠BOC)=![]() ∠AOB,即可得出答案;(4)根据角平分线定义即可求解.
∠AOB,即可得出答案;(4)根据角平分线定义即可求解.
解:当射线OC在∠AOB的内部时,
∵OD,OE分别为∠AOC,∠BOC的角平分线,
∴∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,
∠AOB,
(1)若∠AOB=80°,则∠DOE的度数为40°.
故答案为:40;
(2)∠DOE=∠DOC+∠EOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=∠BOE+∠DOA.
∠BOC=∠BOE+∠DOA.
(3)当射线OC在∠AOB的外部时 (1)中的结论不成立.理由是:
∵OD、OE分别是∠AOC、∠BOC的角平分线
∴∠COD=![]() ∠AOC,
∠AOC,
∠EOC=![]() ∠BOC,
∠BOC,
∠DOE=∠COD∠EOC![]() ∠AOC
∠AOC![]() ∠BOC=∠AOD∠BOE.
∠BOC=∠AOD∠BOE.
(4)∵OD,OE分别为∠AOC,∠BOC的角平分线,
∴∠DOC=∠AOD,∠EOC=∠BOE,
∴∠DOE=∠DOC+∠EOC=∠BOE+∠DOA.
故∠BOE、∠EOD、∠DOA之间数量关系是∠DOE=∠BOE+∠DOA.
故答案为:∠DOE=∠BOE+∠DOA.