题目内容
等边三角形ABC内接于⊙O，如果BD是直径，求∠ACD的度数．
解：∵BD为直径，
∴∠BCD=90°（直径所对的圆周角是直角）；
∵△ABC为等边三角形，
∴∠ACB=60°，
∴∠ACD=∠BCD-∠ACB=90°-60°=30°，即∠ACD=30°．
分析：BD为直径，可知∠BCD=90°，△ABC为等边三角形，可知∠ACB=60°，作差可求∠ACD．
点评：本题考查了圆内接三角形的性质，圆周角定理．解题的关键是明确圆的特殊弦（直径）的性质，特殊三角形的性质．
∴∠BCD=90°（直径所对的圆周角是直角）；
∵△ABC为等边三角形，
∴∠ACB=60°，
∴∠ACD=∠BCD-∠ACB=90°-60°=30°，即∠ACD=30°．
分析：BD为直径，可知∠BCD=90°，△ABC为等边三角形，可知∠ACB=60°，作差可求∠ACD．
点评：本题考查了圆内接三角形的性质，圆周角定理．解题的关键是明确圆的特殊弦（直径）的性质，特殊三角形的性质．
练习册系列答案
相关题目
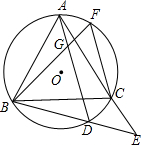如图，等边三角形ABC内接于⊙O，D为
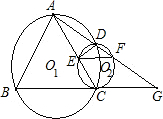如图，已知等边三角形△ABC内接于⊙O1，⊙O2与BC相切于C，与AC相交于E，与⊙O1相交于另一点D，直线AD交⊙O2于另一点F，交BC的延长线于G，点F为AG的中点．对于如下四个结论：①EF∥BC；②BC=FC；③DE•AG=AB•EC；④弧AD=弧DC．其中一定成立的是（ ）
4、如图，等边三角形ABC内接于⊙O，连接OB，OC，那么∠BOC的度数是（ ）
如图，等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO，分别交BC于点P，与⊙O交于点D，连接BD，CD．那么：①四边形BDCO是菱形，②若⊙O的半径为r，三角形的边长为
如图，边长为2