题目内容
如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2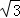 cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)填空:∠CAB=_______°,AO=_________cm;
(2)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并 说明理由;
说明理由;
(3)在点P、Q 运动过程中,求t为何值时,
运动过程中,求t为何值时, .
.

解:(1)30°,10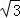
(2)若0<t≤5,则AP=4t,AQ=2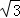 t.
t.
则 =
=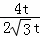 =
= ,
,
又∵AO=10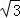 ,AB=20,∴
,AB=20,∴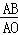 =
=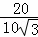 =
= .
.
∴ =
=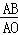 .又∠CAB=30°,∴△APQ∽△ABO.
.又∠CAB=30°,∴△APQ∽△ABO.
∴∠AQP=90°,即PQ⊥AC.
当5<t≤10时,同理,可由△PCQ∽△BCO得∠PQC=90°,即PQ⊥AC.
∴在点P、Q运动过程中,始终有 PQ⊥AC.
PQ⊥AC.
(3)t的值为1s,4s,6s,9s.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目

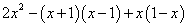 ,其中
,其中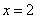 .
.

 内 C.点P在⊙A外 D.点P在⊙A上或外
内 C.点P在⊙A外 D.点P在⊙A上或外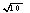
 B. 2
B. 2
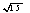

 B.
B.  C.
C. D.
D. 