题目内容
如图已知:直线 交x轴于
交x轴于 点A,交y轴于点
点A,交y轴于点 B,抛物线y=ax2+bx+c经过A(3,0),B(0,3),C(1,0)三点。
B,抛物线y=ax2+bx+c经过A(3,0),B(0,3),C(1,0)三点。
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线 上有一点P,使△ABO与△ADP相似,求出点P的坐标;
上有一点P,使△ABO与△ADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由 .
.
 交x轴于
交x轴于 点A,交y轴于点
点A,交y轴于点 B,抛物线y=ax2+bx+c经过A(3,0),B(0,3),C(1,0)三点。
B,抛物线y=ax2+bx+c经过A(3,0),B(0,3),C(1,0)三点。(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线
 上有一点P,使△ABO与△ADP相似,求出点P的坐标;
上有一点P,使△ABO与△ADP相似,求出点P的坐标; (3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由
 .
.
解:(1)∵抛物线经过A、B、C三点,∴把A(3,0),B(0,3),C(1,0)三点分别代入 得方程组
得方程组 解得:
解得:
∴抛物线的解析式为 :
(2)由题意可得:△ABO为等腰三角形,如图所示,
若△ABO∽△AP1D,则
∴DP1=AD=4 ,∴P1
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,
∵△ABO为等腰三角形, ∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2= P2M,即点M与点C重合,∴P2(1,2)
(3)如图设点E 则
则  ,
,
①当P1(-1,4)时,S四边形AP1CE=S三角形ACP1+S三角形ACE =
= 
∴ ∴
∴
∵点E在x轴下方 ∴
代入得: ,即
,即  ∵△=(-4)2-4 ×7=-12<0
∵△=(-4)2-4 ×7=-12<0
∴此方程无解
②当P2(1,2)时,S四边形AP2CE=S三角形ACP2+S三角形ACE =
∴
∴
∵点E在x轴下方
∴ 代入得:
代入得:
即 ,
,
∵△=(-4)2-4 ×5=-4<0
∴此方程无解
∴此方程无解综上所述,在x轴下方的抛物线上不存在这样的点E.

 得方程组
得方程组 解得:
解得:
∴抛物线的解析式为 :

(2)由题意可得:△ABO为等腰三角形,如图所示,
若△ABO∽△AP1D,则

∴DP1=AD=4 ,∴P1

若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,
∵△ABO为等腰三角形, ∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2= P2M,即点M与点C重合,∴P2(1,2)
(3)如图设点E
 则
则  ,
,①当P1(-1,4)时,S四边形AP1CE=S三角形ACP1+S三角形ACE
 =
= 
∴
 ∴
∴
∵点E在x轴下方 ∴

代入得:
 ,即
,即  ∵△=(-4)2-4 ×7=-12<0
∵△=(-4)2-4 ×7=-12<0∴此方程无解
②当P2(1,2)时,S四边形AP2CE=S三角形ACP2+S三角形ACE =

∴

∴

∵点E在x轴下方
∴
 代入得:
代入得:
即
 ,
,∵△=(-4)2-4 ×5=-4<0
∴此方程无解
∴此方程无解综上所述,在x轴下方的抛物线上不存在这样的点E.


练习册系列答案
相关题目
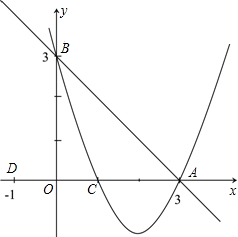 (2012•铜仁地区)如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(2012•铜仁地区)如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.

