题目内容
如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线y=-x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.

【答案】分析:(1)首先确定A、B、C三点的坐标,然后利用待定系数法求抛物线的解析式;
(2)△ABO为等腰直角三角形,若△ADP与之相似,则有两种情形,如答图1所示.利用相似三角形的性质分别求解,避免遗漏;
(3)如答图2所示,分别计算△ADE的面积与四边形APCE的面积,得到面积的表达式.利用面积的相等关系得到一元二次方程,将点E是否存在的问题转化为一元二次方程是否有实数根的问题,从而解决问题.需要注意根据(2)中P点的不同位置分别进行计算,在这两种情况下,一元二次方程的判别式均小于0,即所求的E点均不存在.
解答:解:(1)由题意得,A(3,0),B(0,3)
∵抛物线经过A、B、C三点,
∴把A(3,0),B(0,3),C(1,0)三点分别代入y=ax2+bx+c,
得方程组 …3分
…3分
解得:

∴抛物线的解析式为y=x2-4x+3 …5分
(2)由题意可得:△ABO为等腰三角形,如答图1所示,
若△ABO∽△AP1D,则
∴DP1=AD=4,
∴P1(-1,4)…7分
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,
∵△ABO为等腰三角形,
∴△ADP2是等腰三角形,
由三线合一可得:DM=AM=2=P2M,即点M与点C重合,
∴P2(1,2)…10分
综上所述,点P的坐标为P1(-1,4),P2(1,2);
(3)不存在.
理由:如答图2,设点E(x,y),则
 S△ADE=
S△ADE=
①当P1(-1,4)时,
S四边形AP1CE=S△ACP1+S△ACE= =4+|y|…11分
=4+|y|…11分
∴2|y|=4+|y|,
∴|y|=4
∵点E在x轴下方,
∴y=-4,代入得:x2-4x+3=-4,即x2-4x+7=0,
∵△=(-4)2-4×7=-12<0
∴此方程无解…12分
②当P2(1,2)时,
S四边形AP2CE=S△ACP2+S△ACE= =2+|y|,
=2+|y|,
∴2|y|=2+|y|,
∴|y|=2
∵点E在x轴下方,
∴y=-2,代入得:x2-4x+3=-2,即x2-4x+5=0,
∵△=(-4)2-4×5=-4<0
∴此方程无解
综上所述,在x轴下方的抛物线上不存在这样的点E.…14分
点评:本题重点考查了抛物线的相关性质、相似三角形的性质、图形面积的计算以及一元二次方程根的判别式,涉及的知识点较多.注意在(2)(3)问中,均有两种情形,需要分类讨论计算,避免漏解;(3)问中是否存在点E的问题,转化为一元二次方程实数根个数的问题,需要注意这种解题方法.作为中考压轴题,本题综合性强,难度较大,有利于提高学生的综合解题能力,是一道不错的题目.
(2)△ABO为等腰直角三角形,若△ADP与之相似,则有两种情形,如答图1所示.利用相似三角形的性质分别求解,避免遗漏;
(3)如答图2所示,分别计算△ADE的面积与四边形APCE的面积,得到面积的表达式.利用面积的相等关系得到一元二次方程,将点E是否存在的问题转化为一元二次方程是否有实数根的问题,从而解决问题.需要注意根据(2)中P点的不同位置分别进行计算,在这两种情况下,一元二次方程的判别式均小于0,即所求的E点均不存在.
解答:解:(1)由题意得,A(3,0),B(0,3)
∵抛物线经过A、B、C三点,
∴把A(3,0),B(0,3),C(1,0)三点分别代入y=ax2+bx+c,
得方程组
 …3分
…3分解得:


∴抛物线的解析式为y=x2-4x+3 …5分
(2)由题意可得:△ABO为等腰三角形,如答图1所示,
若△ABO∽△AP1D,则

∴DP1=AD=4,
∴P1(-1,4)…7分
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,
∵△ABO为等腰三角形,
∴△ADP2是等腰三角形,
由三线合一可得:DM=AM=2=P2M,即点M与点C重合,
∴P2(1,2)…10分
综上所述,点P的坐标为P1(-1,4),P2(1,2);
(3)不存在.
理由:如答图2,设点E(x,y),则
 S△ADE=
S△ADE=
①当P1(-1,4)时,
S四边形AP1CE=S△ACP1+S△ACE=
 =4+|y|…11分
=4+|y|…11分∴2|y|=4+|y|,
∴|y|=4
∵点E在x轴下方,
∴y=-4,代入得:x2-4x+3=-4,即x2-4x+7=0,
∵△=(-4)2-4×7=-12<0
∴此方程无解…12分
②当P2(1,2)时,
S四边形AP2CE=S△ACP2+S△ACE=
 =2+|y|,
=2+|y|,∴2|y|=2+|y|,
∴|y|=2
∵点E在x轴下方,
∴y=-2,代入得:x2-4x+3=-2,即x2-4x+5=0,
∵△=(-4)2-4×5=-4<0
∴此方程无解
综上所述,在x轴下方的抛物线上不存在这样的点E.…14分
点评:本题重点考查了抛物线的相关性质、相似三角形的性质、图形面积的计算以及一元二次方程根的判别式,涉及的知识点较多.注意在(2)(3)问中,均有两种情形,需要分类讨论计算,避免漏解;(3)问中是否存在点E的问题,转化为一元二次方程实数根个数的问题,需要注意这种解题方法.作为中考压轴题,本题综合性强,难度较大,有利于提高学生的综合解题能力,是一道不错的题目.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
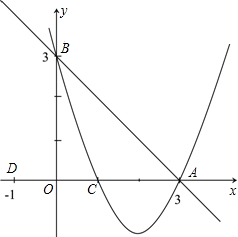 (2012•铜仁地区)如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(2012•铜仁地区)如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点. 为直线
为直线 上一点, 过点
上一点, 过点 、
、 、
、 ,
,  ,
, ,
, ,求
,求 的度数
的度数
 为直线
为直线 上一点, 过点
上一点, 过点 、
、 、
、 ,
,  ,
, ,
, ,求
,求 的度数
的度数
 为直线
为直线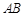 上一点, 过点
上一点, 过点 、
、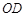 、
、 , 且
, 且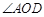 ,
,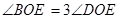 ,
, ,求
,求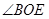 的度数.
的度数.
