题目内容
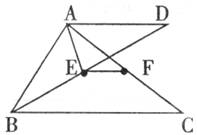
F是△ABC的AC边上一点，AF：FC=1：2，G是BF中点，AG的延长线交BC于点E，则BE：EC= ．
【答案】分析：本题主要应用两三角形相似的判定定理，做题即可．
解答：
解：作FD∥BC
∴△ADF∽△AEC，∠DFG=∠EBG，∠FDG=∠BEG
∵BG=FG
∴△BEG≌△FDG
∴DF=BE
∵AF：FC=1：2
∴DF：EC=AF：AC=1：3
∴BE：EC=1：3
点评：此题考查了相似三角形的判定和性质，①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；③如果两个三角形的两个对应角相等，那么这两个三角形相似．平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似．相似三角形的对应边成比例，对应角相等．
解答：
解：作FD∥BC∴△ADF∽△AEC，∠DFG=∠EBG，∠FDG=∠BEG
∵BG=FG
∴△BEG≌△FDG
∴DF=BE
∵AF：FC=1：2
∴DF：EC=AF：AC=1：3
∴BE：EC=1：3
点评：此题考查了相似三角形的判定和性质，①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；③如果两个三角形的两个对应角相等，那么这两个三角形相似．平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似．相似三角形的对应边成比例，对应角相等．
练习册系列答案
相关题目
中点．
24、阅读材料，解决问题．
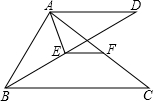
如图所示．P是△ABC的AC边的中点，PQ⊥AC交AB延长线于Q，BR⊥AC于R．
