Question

如下图，点F是△ABC的AC边中点，过点A作BC的平行线，与∠ABC的平分线相交于点D，E为BD的中点。

试探究：（1）AE与BD的位置关系，并给予证明；

（2）EF、AB、BC之间的数量关系，并给予证明。

Answer 1

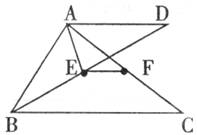
（1）AE⊥BD

证明：∵AD∥BC，∴∠D=∠DBC

∵BD平分∠ABC，∴∠ABD=∠DBC

则∠D=∠ABD，∴AB=AD，即△ABD是等腰三角形            

又∵E是BD的中点，∴AE⊥BD（三线合一） 

（2）EF=（BC－AB）

证明：延长AE交BC于点G（或延长DF）        

由（1）知∠D=∠EBG，∵E是BD中点，∴BE=DE

又∵∠AED=∠GEB，∴△AED≌△GEB（ASA）   

∴AD=GB，AE=GE

又∵F为AC中点，∴EF是AACG的中位线

则EF=GC                                     

∵GC=BC－GB=BC－AD，由（1）知AD=AB

∴GC=BC－AB

∴EF=（BC－AB）