题目内容
 在一个面积为l的正方形中构造一个如下的小正方形:将正方形的各边n等分,然后将每个顶点和它相对顶点最近的分点连接起来,如图所示,若小正方形面积为
在一个面积为l的正方形中构造一个如下的小正方形:将正方形的各边n等分,然后将每个顶点和它相对顶点最近的分点连接起来,如图所示,若小正方形面积为 ,求n的值.
,求n的值.
 解:A1B=
解:A1B= ,CC1=
,CC1= ,A1C=
,A1C= ,
,过C1作C1P⊥A1C于P,则Rt△A1BC∽Rt△CPC1,
得C1P=
 =
= .
.∵S面=
 ,∴C1P2=
,∴C1P2= =
= ,
,得(n-41)(n+40)=0,故n₁=41,n₂=-40(舍去).
故答案为:41.
分析:根据已知条件可得A1B=
 ,CC1=
,CC1= ,A1C=
,A1C= ,然后过C1作
,然后过C1作C1P⊥A1C于P,利用Rt△A1BC∽Rt△CPC1,可得C1P,将小正方形面积为
 ,代入即可得出答案.
,代入即可得出答案.点评:此题主要考查学生对相似三角形的判定与性质,勾股定理,正方形的性质等知识点的理解与掌握,解答此题的关键是
过C1作C1P⊥A1C于P,利用Rt△A1BC∽Rt△CPC1,求得C1P,这是此题的突破点.

练习册系列答案
相关题目
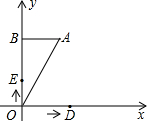 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
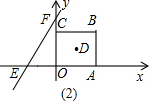

 如图,A、B两点的坐标分别为(-3,0)、(0,3),C点在x轴的正半轴上,且到原点的距离为1.点P、Q分别从A、B两点同时出发,以相同的速度分别向x轴、y轴的正方向作匀速直线运动,直线PQ交直线AB于D.
如图,A、B两点的坐标分别为(-3,0)、(0,3),C点在x轴的正半轴上,且到原点的距离为1.点P、Q分别从A、B两点同时出发,以相同的速度分别向x轴、y轴的正方向作匀速直线运动,直线PQ交直线AB于D. (2013•恩施州)如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( )
(2013•恩施州)如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( )