题目内容
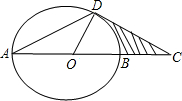
如图，AB为半圆O的直径，C是半圆上一点，且∠COA=60°，设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3，则它们之间的关系是（ ）
| A．S1＜S2＜S3 | B．S2＜S1＜S3 | C．S1＜S3＜S2 | D．S3＜S2＜S1 |
作OD⊥BC交BC与点D，∵∠COA=60°，
∴∠COB=120°，则∠COD=60°．
∴S扇形AOC=
=
；
S扇形BOC=
=
．
在三角形OCD中，∠OCD=30°，
∴OD=
，CD=
，BC=
R，
∴S△OBC=
，S弓形=
-
=
，
＞
＞
，∴S2＜S1＜S3
故选B．
∴∠COB=120°，则∠COD=60°．
∴S扇形AOC=
| 60πR2 |
| 360 |
| πR2 |
| 6 |
S扇形BOC=
| 120πR2 |
| 360 |
| πR2 |
| 3 |
在三角形OCD中，∠OCD=30°，
∴OD=
| R |
| 2 |
| ||
| 2 |
| 3 |
∴S△OBC=
| ||
| 4 |
| πR2 |
| 3 |
| ||
| 4 |
(4π-3
| ||
| 12 |
(4π-3
| ||
| 12 |
| πR2 |
| 6 |
| ||
| 4 |
故选B．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
P到弦MN的距离为x．
