Question

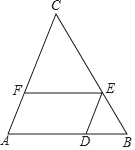
【题目】如图，已知△ABC中，D、E、F分别是边AB、BC、CA上的点，且EF∥AB， =2．

（1）设，．试用、表示；

（2）如果△ABC的面积是9，求四边形ADEF的面积．

Answer 1

【答案】（1）；（2）4.

【解析】分析：（1）由EF∥AB知=，据此可得==2，即==，从而证△BDE∽△BAC得∠BDE=∠A，即可知DE∥AC、四边形ADEF是平行四边形，再利用====及平行四边形法则可得答案；

（2）由EF∥AB、DE∥AC知△CFE∽△CAB，△BDE∽△BAC，从而得=（）2==（）2=，进一步得出S△CFE=4、S△BDE=1，从而得出答案．

详解：（1）∵EF∥AB，∴=

=2，∴==2，∴==．

∵∠B=∠B，∴△BDE∽△BAC，

∴∠BDE=∠A，∴DE∥AC，则四边形ADEF是平行四边形．

∵=

====，则=+=+；

（2）由（1）知=、=．

∵EF∥AB，DE∥AC，

∴△CFE∽△CAB，△BDE∽△BAC，

∴=（）2==（）2=．

∵S△ABC=9，∴S△CFE=4、S△BDE=1，

∴四边形ADEF的面积=S△ABC﹣S△CFE﹣S△BDE=4．