题目内容
各边都是整数,且最大边长为12的三角形的个数有________个.
42
分析:根据题意,设较小的两边长为x、y且x≤y,可得关系式x≤y≤12,x+y>12,x、y∈N*;分别令x=1、2、3、4、5…、12,分别求得y的可取值,由分类计数原理,计算可得答案.
解答:设较小的两边长为x、y且x≤y,
则x≤y≤12,x+y>12,x、y∈N*.
当x=1时,y=12;
当x=2时,y=11,12;
当x=3时,y=10,11,12;
当x=4时,y=9,10,11,12;
当x=5时,y=8,9,10,11,12;
当x=6时,y=7,8,9,10,11,12;
当x=7时,y=7,8,9,10,11,12;
…
当x=12时,y=12.
所以不同三角形的个数为1+2+3+4+5+6+6+5+4+3+2+1=42.
故答案为:42.
点评:本题关键是列出约束条件,然后寻找x=1,2,…,12时,y的取值个数的规律,再用分类计数原理求解.
分析:根据题意,设较小的两边长为x、y且x≤y,可得关系式x≤y≤12,x+y>12,x、y∈N*;分别令x=1、2、3、4、5…、12,分别求得y的可取值,由分类计数原理,计算可得答案.
解答:设较小的两边长为x、y且x≤y,
则x≤y≤12,x+y>12,x、y∈N*.
当x=1时,y=12;
当x=2时,y=11,12;
当x=3时,y=10,11,12;
当x=4时,y=9,10,11,12;
当x=5时,y=8,9,10,11,12;
当x=6时,y=7,8,9,10,11,12;
当x=7时,y=7,8,9,10,11,12;
…
当x=12时,y=12.
所以不同三角形的个数为1+2+3+4+5+6+6+5+4+3+2+1=42.
故答案为:42.
点评:本题关键是列出约束条件,然后寻找x=1,2,…,12时,y的取值个数的规律,再用分类计数原理求解.

练习册系列答案
相关题目
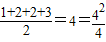 种不同的取法.
种不同的取法.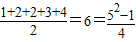 种不同的取法.
种不同的取法.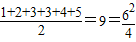 种不同的取法.
种不同的取法.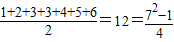 种不同的取法…
种不同的取法…