题目内容
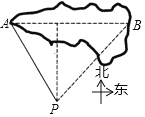
【题目】在数学活动课上，九年级（1）班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离．现测得亭子A位于点P北偏西30°方向，亭子B位于点P北偏东α方向，测得点P与亭子A之间的距离为200米．则亭子A与亭子B之间的距离为（ ）
A.100+100
sinα米B.100+100tanα米
C.100+
米D.100+
米
【答案】B
【解析】
直接利用直角三角形的性质结合锐角三角函数关系得出PC，BC的长，进而得出答案．
解：过点P作PC⊥AB于点C，
由题意可得：∠APC＝30°，PA＝200m，∠CPB＝α，
则AC＝
AP＝100m，PC＝PA×cos30°＝100
米，
故tanα＝
＝
，
则BC＝100tanα米，
故AB＝AC+BC＝（100+100tanα）米．
故选：B．
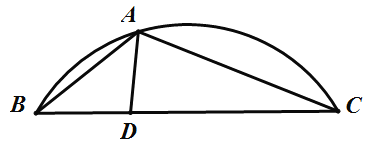
【题目】如图，A是
上一动点，D是弦BC上一定点，连接AB，AC，AD．设线段AB的长是xcm，线段AC的长是
cm，线段AD的长是
cm．
小腾根据学习函数的经验，分别对函数，随自变量x的变化的关系进行了探究．下面是小腾的探究过程，请补充完整：
（1）对于点A在上的不同位置，画图、测量，得到了，的长度与x的几组值：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
x/cm | 0.00 | 0.99 | 2.01 | 3.46 | 4.98 | 5.84 | 7.07 | 8.00 |
| 8.00 | 7.46 | 6.81 | 5.69 | 4.26 | 3.29 | 1.62 | 0.00 |
| 2.50 | 2.08 | 1.88 | 2.15 | 2.99 | 3.61 | 4.62 | m |
请直接写出上表中的m值是 ；
（2）在同一平面直角坐标系
中，描出补全后表中各组数据所对应的点(x，)，(x，)，并画出函数，的图象；
（3）结合函数图象，解决问题：当AC=AD时，AB的长度约为 cm；当AC=2AD时，AB的长度约为 cm．
