题目内容
如图,抛物线 与直线
与直线 交于
交于 两点,交
两点,交 轴与
轴与 两点,连接
两点,连接 ,已知
,已知 .
.
(1)求抛物线的解析式;
(2)求 的值;
的值;
|
 为点
为点 下方、
下方、 轴上方、
轴上方、 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接 ,过点
,过点 作
作 交
交 轴于点
轴于点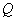 ,问:是否存在点
,问:是否存在点 使得以
使得以 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由 .
的坐标;若不存在,请说明理由 . 第27题图
解:(1)把A(0,3),C(3,0)代入 得
得
 ------------------------------1分
------------------------------1分
解得

∴抛物线的解析式为 ;--------------2分
;--------------2分
 (2)如图1,过点B作BH⊥x轴于H,
(2)如图1,过点B作BH⊥x轴于H,
解方程组
得: 或
或
∴点B的坐标为(4,1) ---------------------3分
又∵C(3,0)
∴ ,
, ,
, ,
,
∴
∵
∴
同理: ---------------------4分
---------------------4分
∴
∴
 ;-------------------------------------5分
;-------------------------------------5分
(3)存在点P,使得以A,P,Q为顶点的三角形与 相似.
相似.
过点P作PG⊥y轴于G,则 ,设点P的横坐标为x,由于P在y轴右侧可得x>0,则
,设点P的横坐标为x,由于P在y轴右侧可得x>0,则 ,
,
∵PQ⊥PA,
 , ---------------------------------------6分
, ---------------------------------------6分
 ①如图2,当
①如图2,当 时,
时, .
.
∵ ,
,
∴
∴
∴
∴P(x,3﹣3x) ---------------------7分
把P(x,3﹣3x)代入 ,得
,得

整理,得

 解得:
解得: (舍去),
(舍去), (舍去);---------8分
(舍去);---------8分
②如图3,当 时,
时,
同理可得: ,
,
则P ----------------------------9分
----------------------------9分
把P ,代入
,代入 ,得
,得

整理,得

解得: (舍去),
(舍去),
∴ ---------------------------------------10分
---------------------------------------10分

某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
| 时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
| 行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较 与
与 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.



 是
是 的直径,
的直径,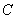 ,
, 两点在
两点在 ,则
,则 的度数为 .
的度数为 .
 与
与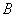 两点,与
两点,与 .
. ;
; ,求四边形
,求四边形 的面积.
的面积.
 元 B.
元 B. 元 C.
元 C. 元 D.
元 D. 元
元