Question

如图：为台球桌面矩形ABCD示意图，AB=2m，AD=1.5m，E为AD边上任意一点，一球以E点出发经三边碰撞又回到E点，（以E到F到G到H到E）不计球的大小，则球经过的线路长是

5m

．

Answer 1

分析：分别作E点关于AB、CD的对称点，设为E₁，E₂，作E₁，E₂的垂直平分线，交BC于G点，连接GE₂交CD于H点，连接GE₁交AB于F点，则路线长等于EFGH四边形周长，也等于2倍的GE₁的长度，再利用勾股定理求出GE₁的长度即可．

解答：解：已知如图所示：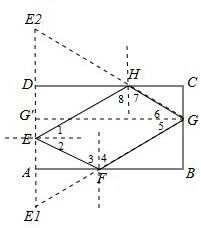
作E点关于AB、CD的对称点，设为E₁，E₂，
∴HE₂=HE，FE₁=EF，
作E₁，E₂的垂直平分线，交BC于G点，连接GE₂交CD于H点，连接GE₁交AB于F点，
∴EF+FG+HG+EH=E₂G+E₁G=2GE₁，
在Rt△G′E₁G中，GE₁=

2 2+ ( 3 2 ) 2

=

5

2

，
∴球经过的线路长是=2×

5

2

=5，
故答案为：5m．

点评：本题考查了矩形的性质，勾股定理以及轴对称的性质，解题的关键是分别作E点关于AB、CD的对称点，作E₁，E₂的垂直平分线得到相等的线段．