题目内容
 如图,⊙O的直径CD垂直于弦AB,∠BDC=24°.则∠AOC= °.
如图,⊙O的直径CD垂直于弦AB,∠BDC=24°.则∠AOC= °.
- A.24
- B.48
- C.96
- D.36
B
分析:连接OB,利用圆周角定理即可求得∠BOC的度数,然后利于垂径定理证得 ,根据等弧所对的圆周角相等,即可求解.
,根据等弧所对的圆周角相等,即可求解.
解答: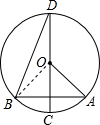 解:连接OB.
解:连接OB.
∠BOC=2∠BDC=48°,
∵⊙O的直径CD垂直于弦AB,
∴ ,
,
∴∠AOC=∠BOC=48°.
故选B.
点评:本题考查了垂径定理、圆周角定理、以及弧,圆心角之间的关系,是一个基础题.
分析:连接OB,利用圆周角定理即可求得∠BOC的度数,然后利于垂径定理证得
 ,根据等弧所对的圆周角相等,即可求解.
,根据等弧所对的圆周角相等,即可求解.解答:
 解:连接OB.
解:连接OB.∠BOC=2∠BDC=48°,
∵⊙O的直径CD垂直于弦AB,
∴
 ,
,∴∠AOC=∠BOC=48°.
故选B.
点评:本题考查了垂径定理、圆周角定理、以及弧,圆心角之间的关系,是一个基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )| A、80° | B、50° | C、40° | D、20° |
 如图,⊙O的直径CD过弦EF的中点G,∠OEF=34°,则∠DCF的度数是
如图,⊙O的直径CD过弦EF的中点G,∠OEF=34°,则∠DCF的度数是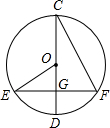 如图,⊙O的直径CD过弦EF的中点G,∠EOG=60°,则∠DCF的度数为
如图,⊙O的直径CD过弦EF的中点G,∠EOG=60°,则∠DCF的度数为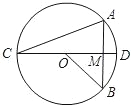 如图,⊙O的直径CD过弦AB的中点M,∠ACD=28°,则∠B=
如图,⊙O的直径CD过弦AB的中点M,∠ACD=28°,则∠B=