题目内容
 a、如图1,在平行四边形ABCD中,E是AD的中点,CE与BA的延长线相交于F点.连结DF.(1)求证:四边形ACDF是平行四边形.(2)若ACDF是矩形,试探求∠1与∠2之间的关系.b、如图2,等腰梯形ABCD中,E、F是两腰的中点,连接线段AF,作EG∥AF,交BC于G,再连结线段FG.(1)求证:四边形AEGF是平行四边形.(2)若AEGF是矩形,试探求∠1与∠2之间的关系.
a、如图1,在平行四边形ABCD中,E是AD的中点,CE与BA的延长线相交于F点.连结DF.(1)求证:四边形ACDF是平行四边形.(2)若ACDF是矩形,试探求∠1与∠2之间的关系.b、如图2,等腰梯形ABCD中,E、F是两腰的中点,连接线段AF,作EG∥AF,交BC于G,再连结线段FG.(1)求证:四边形AEGF是平行四边形.(2)若AEGF是矩形,试探求∠1与∠2之间的关系.
a、如图1.
(1)证明:∵平行四边形ABCD中,E是AD的中点,
∴AE=ED,BF∥CD,
∴∠FAE=∠CDE.
在△AEF与△DEC中,
 ,
,
∴△AEF≌△DEC,
∴AF=CD,
又BF∥CD,即AF∥CD,
∴四边形ACDF是平行四边形;
 (2)解:∠1=2∠2.理由如下:
(2)解:∠1=2∠2.理由如下:
∵ACDF是矩形,
∴AE=CE,
∴∠EAC=∠ECA,
又∵平行四边形ABCD中,AD∥BC,
∴∠EAC=∠2,
∴∠EAC=∠ECA=∠2,
∴∠1=∠EAC+∠ECA=∠2+∠2=2∠2.
 b、如图2.
b、如图2.
(1)证明:∵等腰梯形ABCD中,E、F是两腰的中点,
∴EF为梯形ABCD的中位线,
∴EF∥BC,
又∵EG∥AF,
∴∠AFE=∠FEG=∠2,∠BAF=∠BEG.
在△AEF与△EBG中,
 ,
,
∴△AEF≌△EBG,
∴AF=EG,
∵AF∥EG,
∴四边形AEGF是平行四边形;
(2)解:∠1=2∠2.理由如下:
理由是:∵AEGF是矩形,
∴FG∥AB,∠AEG=∠EGF=90°,
∴∠B=∠C=∠FGC,
∵∠2+∠B=90°,2∠B+∠1=180°,
∴2∠B+∠1=2(∠2+∠B)=180°,
∴∠1=2∠2.
分析:a、(1)由已知平行四边形ABCD中,E是AD的中点,可得AE=ED,BF∥CD,则∠FAE=∠CDE,又∠AEF=∠DEC,利用ASA证明△AEF≌△DEC,所以AF=CD,再根据“一组对边平行且相等的四边形是平行四边形”证得其为平行四边形;
(2)根据矩形的性质得AE=CE,则∠EAC=∠ECA,又由平行四边形ABCD得∠EAC=∠2,所以∠EAC=∠ECA=∠2,从而得∠1=∠EAC+∠ECA=∠2+∠2=2∠2.
b、(1)根据平行线的性质推出∠AFE=∠FEG=∠2,∠BAF=∠BEG,又AE=EB,利用AAS证明△AEF≌△EBG,推出AF=EG,再根据“一组对边平行且相等的四边形是平行四边形”证得其为平行四边形;
(2)根据矩形的性质得FG∥AB,∠AEG=∠EGF=90°,由等腰梯形及等腰三角形的性质得∠B=∠C=∠FGC,再根据三角形的内角和定理得∠2+∠B=90°,2∠B+∠1=180°,变形即可得出∠1=2∠2.
点评:本题主要考查对等腰梯形的性质,平行四边形的判定与性质,矩形的性质,全等三角形的性质和判定,三角形的内角和定理等知识点的理解和掌握,能推出(1)AF=CD,(2)AF=EG是解题的关键.
(1)证明:∵平行四边形ABCD中,E是AD的中点,
∴AE=ED,BF∥CD,
∴∠FAE=∠CDE.
在△AEF与△DEC中,
 ,
,∴△AEF≌△DEC,
∴AF=CD,
又BF∥CD,即AF∥CD,
∴四边形ACDF是平行四边形;
 (2)解:∠1=2∠2.理由如下:
(2)解:∠1=2∠2.理由如下:∵ACDF是矩形,
∴AE=CE,
∴∠EAC=∠ECA,
又∵平行四边形ABCD中,AD∥BC,
∴∠EAC=∠2,
∴∠EAC=∠ECA=∠2,
∴∠1=∠EAC+∠ECA=∠2+∠2=2∠2.
 b、如图2.
b、如图2.(1)证明:∵等腰梯形ABCD中,E、F是两腰的中点,
∴EF为梯形ABCD的中位线,
∴EF∥BC,
又∵EG∥AF,
∴∠AFE=∠FEG=∠2,∠BAF=∠BEG.
在△AEF与△EBG中,
 ,
,∴△AEF≌△EBG,
∴AF=EG,
∵AF∥EG,
∴四边形AEGF是平行四边形;
(2)解:∠1=2∠2.理由如下:
理由是:∵AEGF是矩形,
∴FG∥AB,∠AEG=∠EGF=90°,
∴∠B=∠C=∠FGC,
∵∠2+∠B=90°,2∠B+∠1=180°,
∴2∠B+∠1=2(∠2+∠B)=180°,
∴∠1=2∠2.
分析:a、(1)由已知平行四边形ABCD中,E是AD的中点,可得AE=ED,BF∥CD,则∠FAE=∠CDE,又∠AEF=∠DEC,利用ASA证明△AEF≌△DEC,所以AF=CD,再根据“一组对边平行且相等的四边形是平行四边形”证得其为平行四边形;
(2)根据矩形的性质得AE=CE,则∠EAC=∠ECA,又由平行四边形ABCD得∠EAC=∠2,所以∠EAC=∠ECA=∠2,从而得∠1=∠EAC+∠ECA=∠2+∠2=2∠2.
b、(1)根据平行线的性质推出∠AFE=∠FEG=∠2,∠BAF=∠BEG,又AE=EB,利用AAS证明△AEF≌△EBG,推出AF=EG,再根据“一组对边平行且相等的四边形是平行四边形”证得其为平行四边形;
(2)根据矩形的性质得FG∥AB,∠AEG=∠EGF=90°,由等腰梯形及等腰三角形的性质得∠B=∠C=∠FGC,再根据三角形的内角和定理得∠2+∠B=90°,2∠B+∠1=180°,变形即可得出∠1=2∠2.
点评:本题主要考查对等腰梯形的性质,平行四边形的判定与性质,矩形的性质,全等三角形的性质和判定,三角形的内角和定理等知识点的理解和掌握,能推出(1)AF=CD,(2)AF=EG是解题的关键.

练习册系列答案
相关题目
 22、如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
22、如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)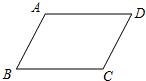 17、如图,请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°中,选出两个,推出四边形ABCD是平行四边形:
17、如图,请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°中,选出两个,推出四边形ABCD是平行四边形:
 ∥
∥ ,②
,② ,③
,③ ,④
,④ 中,选出两个恰当的关系作为条件,推出四边形
中,选出两个恰当的关系作为条件,推出四边形 是平行四边形 ★
.(写出一种即可)
是平行四边形 ★
.(写出一种即可)
 是平行四边形,并予以证明.(写出一种即可)关系:①
是平行四边形,并予以证明.(写出一种即可)关系:① ∥
∥ ,②
,② ,③
,③ ,④
,④ .
.
 中, , ;
中, , ;