Question

如图，直线y=-

3

3

x+2与x轴相交于点A，与y轴相交于点B，将△ABO沿着AB翻折，得到△ABC，则点C的坐标为

 

．

Answer 1

分析：由已知条件不难求出点A、点B的坐标，从而求得AB的大小，由于将△ABO沿着AB翻折，得到△ABC，可得CO⊥AB，得到角度后利用直角三角形求解点C的坐标．

解答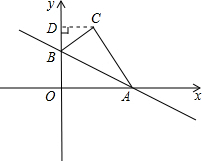：解：过点C作CD⊥y轴于D，
∵直线y=-

3

3

x+2与x轴相交于点A，与y轴相交于点B，
∴BC=OB=2，OA=2

3

，AB=

22+(2 3 )2

=4，
∴∠BAO=30°，
∠DBC=∠CBA=∠ABO=90°-30°=60°，
∴Rt△DBC中，
BD=

1

2

BC=

1

2

×2=1，
∴OD=1+2=3，
CD=

22-12

=

3

∴C（

3

，3）．
故填（

3

，3）．

点评：本题考查了一次函数的综合应用；图形的翻折问题要找准对应量，进行线段与角的等效转移，利用直角三角形求解是正确解答本题的关键．