题目内容
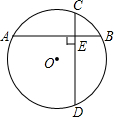
如图所示，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，则⊙O的半径为______cm．
连接OC，
设AP=x，则PB=5x，
∴OP=3x-x=2x．
∵CD⊥AB，∴PC=
CD=
×10=5．
在Rt△PCO中，OC2-OP2=PC2，
∴（3x）2-（2x）2=52，
∴x=
，∴⊙O的半径为3
cm．
设AP=x，则PB=5x，
∴OP=3x-x=2x．
∵CD⊥AB，∴PC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PCO中，OC2-OP2=PC2，
∴（3x）2-（2x）2=52，
∴x=
| 5 |
| 5 |
练习册系列答案
相关题目
