题目内容
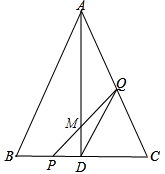
如图，面积为13cm2的△ABC沿BC方向平移至△DEF的位置，平移的距离是BC的长的2倍，图中四边形ACED的面积为
- A.26cm2
- B.39cm2
- C.13cm2
- D.52cm2
B
分析：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
解答：设点A到BC的距离为h，则S△ABC=
BC•h=13cm2，
∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×13=39cm2．
故选B．
点评：本题考查了平移的性质，三角形的面积，主要用了对应点间的距离等于平移的距离的性质．
分析：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
解答：设点A到BC的距离为h，则S△ABC=
BC•h=13cm2，∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=
（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×13=39cm2．故选B．
点评：本题考查了平移的性质，三角形的面积，主要用了对应点间的距离等于平移的距离的性质．
练习册系列答案
相关题目
如图，一块草坪的形状为四边形ABCD，其中∠B=90°，AB=3cm，BC=4cm，CD=12cm，AD=13cm，求这块草坪的面积．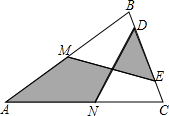
如图，在△ABC中，AB=AC．M、N分别是AB、AC的中点，D、E为BC上的点，连接DN、EM．若AB=13cm，BC=10cm，DE=5cm，则图中阴影部分的面积为
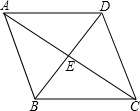如图所示，四边形ABCD是边长为13cm的菱形，其中对角线BD长10cm，求：
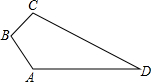如图，在四边形ABCD中，已知AB=4cm，BC=3cm，AD=12cm，DC=13cm，∠B=90°，则四边形ABCD的面积为