题目内容
如图，
、
分别切⊙
于点
、
，点
是⊙上一点且
，则
____度．
60
解析试题分析：连接OA、OB，根据切线的性质可得∠PAO=∠PBO=90°，根据圆周角定理可得∠AOB的度数，再根据四边形的内角和定理求解即可.
连接OA、OB
∵、分别切⊙于点、
∴∠PAO=∠PBO=90°
∵
∴∠AOB=120°
∴360°-90°-90°-120°=60°.
考点：切线的性质，圆周角定理，四边形的内角和定理
点评：解题的关键是熟练掌握切线垂直于经过切点的半径；在同圆或等圆中，同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.
练习册系列答案
相关题目
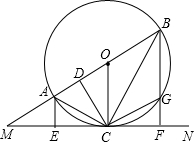，BF⊥MN，E、F分别为垂足，BF交⊙O于G，连接AC、BC，过点C作CD⊥AB，D为垂足，连接OC、CG．下列结论，其中正确的有（ ）
如图，直线AC切⊙O于点A，点B在⊙O上，且AB=AC=AO，OC、BC分别交⊙O于点E、F．求证：EF是圆内接正二十四边形的一边．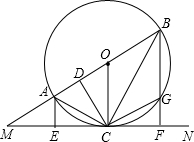
，BF⊥MN，E、F分别为垂足，BF交⊙O于G，连接AC、BC，过点C作CD⊥AB，D为垂足，连接OC、CG．下列结论，其中正确的有
如图，直线AC切⊙O于点A，点B在⊙O上，且AB=AC=AO，OC、BC分别交⊙O于点E、F．求证：EF是圆内接正二十四边形的一边．