Question

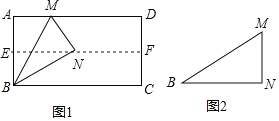
【题目】如图，在矩形纸片ABCD中，AB＝3，BC＝2，沿对角线AC剪开（如图①）；固定△ADC，把△ABC沿AD方向平移（如图②），当两个三角形重叠部分的面积最大时，移动的距离AA′等于（ ）

A. 1 B. 1.5 C. 2 D. 0.8或1.2

Answer 1

【答案】A

【解析】分析：设AA′=x，先证△AA'E∽△ADC，利用相似的性质用含x代数式表示出A′E，再根据阴影部分为平行四边形利用面积建立二次函数解析式，通过最值即可得出答案.

详解：如图所示，

设AA′=x，则DA′=2-x，

∵四边形ABCD是矩形，

∴CD=AB=3，AD=BC=2，

∵EA′∥CD，

∴△AA'E∽△ADC，

∴，

即，

∴A′E=x，

∵EA′∥CD，CA′∥CA，

∴阴影部分为平行四边形，

∴阴影部分的面积：

S=EA′·DA′=，

即当，阴影部分的面积最大为，

∴当平移的距离AA′=1时，两个三角形重叠部分的面积最大.

故选A．