题目内容
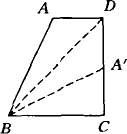
已知如图所示,梯形ABCD中,AB∥DC,AD=BC,延长AB到E,使BE=DC.求证AC=CE.
答案:
解析:
解析:
|
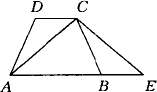
证法1:∵四边形ABCD是等腰梯形, ∴∠ADC=∠BCD. 又∵DC∥AB, ∴∠DCB=∠CBE. 在△ADC与△CBE中,AD=BC,∠ADC=∠CBE,DC=BE, ∴△ADC≌△CBE.∴AC=CE. 证法2:如图所示,连结DB,
∵DC∥BE,DC=BE, ∴四边形DCEB为平行四边形.∴DB=CE. 又∵四边形ABCD为等腰梯形, ∴AC=DB.∴AC=CE. 证法3:如图所示,作CF⊥AE于F,
DM⊥AE于M,在△AMD与△BFC中, ∠DAM=∠CBF,AD=BC,∠DMA=∠CFB=90°, ∴△AMD≌△BFC.∴AM=BF. 又∵DC=BE, ∴AM+MF=BF+BE. ∴F为AE中点,CF为AE的垂直平分线. ∴AC=EC. 证法4:如图所示,连结BD,
∵DC∥AB,DC=BE, ∴四边形BECD为平行四边形. ∴∠2=∠3. 又四边形ABCD是等腰梯形, ∴AC=BD. 又∵AD=BC,AB=AB, ∴△ABC≌△BAD. ∴∠1=∠2. ∴∠1=∠3,∴AC=CE. 分析:本题的证法很多.(1)由于AC与CE具有相同端点C,并且构成了△ACE,所以只需证CA=CE即可.(2)欲证AC=CE,选择一个中间量DB,证AC=DB,CE=DB即可.(3)借助线段垂直平分线的性质证AC=CE.(4)欲证AC=CE,只需证∠1=∠3,欲证∠1=∠3,只需找一中间角∠2,使∠1=∠2,∠2=∠3,所以∠1-∠3即可得证. |

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目



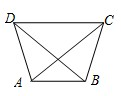 已知如图所示,梯形ABCD中AB∥CD,AD=BC,AC⊥BD,AB=3,CD=5,则梯形的面积是
已知如图所示,梯形ABCD中AB∥CD,AD=BC,AC⊥BD,AB=3,CD=5,则梯形的面积是