Question

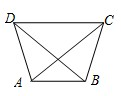已知如图所示，梯形ABCD中AB∥CD，AD=BC，AC⊥BD，AB=3，CD=5，则梯形的面积是

 

．

Answer 1

分析：过点C作CE∥BD交AB于点E，作CF⊥AE于F，从而可得到∠ACE=90°，根据等腰直角三角形的性质可求得CF的长，此时再求梯形的面积就不难了．

解答：解：过点C作CE∥BD交AB于点E，得平行四边形BDCE．
则∠ACE=90°，CE=BD=AC，BE=CD=5，
作CF⊥AE于F，
根据等腰直角三角形的性质，得CF=

1

2

AE=4，
则梯形的面积就是三角形ACE的面积=

1

2

×8×4=16．

点评：此题通过平移对角线发现一个平行四边形和一个等腰直角三角形，能够把梯形的面积转化为三角形的面积进行求解．