Question

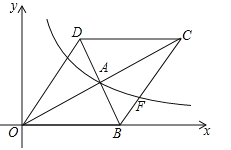
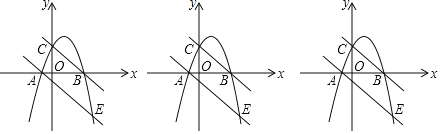
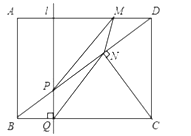
【题目】如图，在平面直角坐标系中，直线交轴于点，交轴于，抛物线经过点、，且与轴交于另一点．

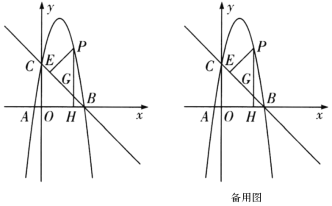
（1）求抛物线的解析式；

（2）点为第一象限内抛物线上一动点，过点作轴于点，交直线于点，设点的横坐标为．

①过点作于点，设的长度为，请用含的式子表示，并求出当取得最大值时，点的坐标．

②在①的条件下，当直线到直线的距离等于时，请直接写出符合要求的直线的解析式．

Answer 1

【答案】（1）；（2）①，点坐标为，②或．

【解析】

（1）根据直线BC求出点B、C的坐标，用待定系数法即可求出抛物线解析式；

（2）①过点作于点，推出，再设点，，得出PE后即可得出答案；②根据①z中得出的h值，代入两直线的距离公式即可．

解：（1）在直线中，令，得；令，得，

∴、

把点，的坐标代入抛物线解析式中，得

解得

∴抛物线解析式为

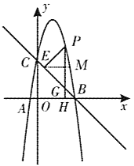
（2）①如解图，过点作于点.

∴

∵，

∴

∴

又∵

∴

∵

∴是等腰直角三角形

∴

设点，

∴

则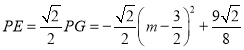

即：.

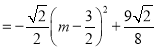∴当时，取得最大值

此时点坐标为

②直线BC的解析式为：

直线的解析式为：

由题意可得，两直线间的距离为：

根据两直线间的距离公式可得：

解得：

直线的解析式为：或．