题目内容
阅读材料1:
对于两个正实数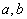 ,由于
,由于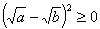 ,所以
,所以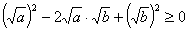 ,即
,即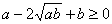 ,所以得到
,所以得到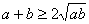 ,并且当
,并且当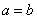 时,
时,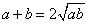 .
.
阅读材料2:
若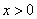 ,则
,则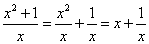 ,因为
,因为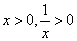 ,所以由阅读材料1可得,
,所以由阅读材料1可得,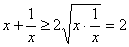 ,即
,即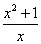 的最小值是2,只有
的最小值是2,只有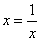 时,即
时,即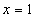 时取得最小值.
时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小:
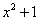
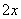 (其中
(其中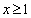 );
); 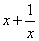
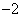 (其中
(其中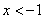 )
)
(2)已知代数式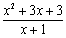 变形为
变形为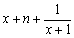 ,求常数n的值;
,求常数n的值;
(3)当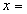 时,
时,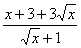 有最小值,最小值为 . (直接写出答案)
有最小值,最小值为 . (直接写出答案)
(1)比较大小:

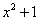 ≥
≥ 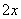 (其中
(其中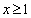 );
); 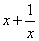 ____
____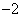 (其中
(其中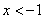 )
)
(2)解: 


∴
(3)当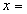 0 时,
0 时,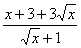 有最小值,最小值为 3 . (直接写出答案)
有最小值,最小值为 3 . (直接写出答案)

练习册系列答案
相关题目
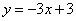 与
与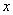 轴、
轴、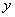 轴分别交于
轴分别交于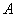 、
、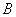 两点,以
两点,以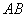 为边在第一象限作正方形
为边在第一象限作正方形 ,点
,点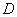 在双曲线
在双曲线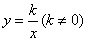 上.将正方形沿
上.将正方形沿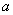 个单位长度后,点
个单位长度后,点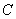 恰好落在该双曲线上,则
恰好落在该双曲线上,则 ;
;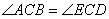 ,则可以用_______公理(或定理)判定全等.
,则可以用_______公理(或定理)判定全等.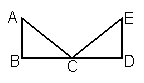
 .
. 
 >0
>0 __________﹣
__________﹣ (用“>”、“=”和“<”连接)
(用“>”、“=”和“<”连接) ,则﹣2★﹣4=__________.
,则﹣2★﹣4=__________.